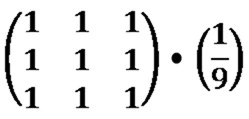Edge enhance | Software by Default

Posts Tagged 'Edge enhance'

C# How to: Fuzzy Blur Filter

Article Purpose

This article serves to illustrate the concepts involved in implementing a Fuzzy Blur Filter. This filter results in rendering non-photo realistic images which express a certain artistic effect.

Frog: Filter Size 19×19

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample source code accompanying this article includes a Windows Forms based test application. The concepts explored throughout this article can be replicated/tested using the sample application.

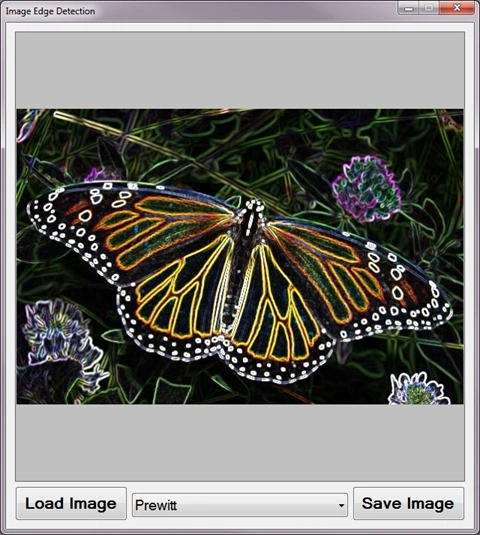
When executing the sample application the user interface exposes a number of configurable options:

Loading and Saving Images – Users are able to load source/input images from the local file system by clicking the Load Image button. Clicking the Save Image button allow users to save filter result images.
Filter Size – The specified filter size affects the filter intensity. Smaller filter sizes result in less blurry images being rendered, whereas larger filter sizes result in more blurry images being rendered.
Edge Factors – The contrast of fuzzy image noise expressed in resulting images depend on the specified edge factor values. Values less than one result in detected image edges being darkened and values greater than one result in detected image edges being lightened.

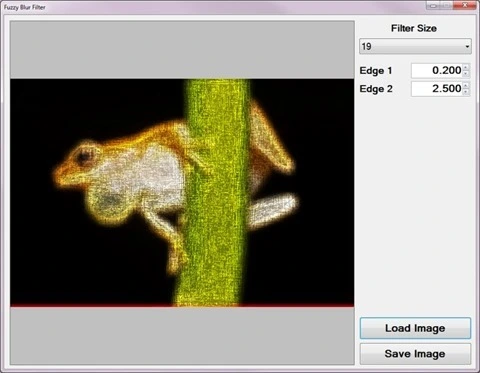
The following image is a screenshot of the Fuzzy Blur Filter sample application in action:

Frog: Filter Size 9×9

Fuzzy Blur Overview

The Fuzzy Blur Filter relies on the interference of image noise when performing edge detection in order to create a fuzzy effect. In addition image blurring results from performing a mean filter.

The steps involved in performing a Fuzzy Blur Filter can be described as follows:

Edge Detection and Enhancement – Using the first edge factor specified enhance image edges by performing Boolean Edge detection. Being sensitive to image noise, a fair amount of detected image edges will actually be image noise in addition to actual image edges.
Mean Filter Blur – Using the edge enhanced image created in the previous step perform a mean filter blur. The enhanced edges will be blurred since a Mean filter does not have edge preservation properties. The size of the Mean filter implemented depends on a user specified value.
Edge Detection and Enhancement – Using the Mean filter blurred image created in the previous step once again perform Boolean Edge detection, enhancing detected edges according to the second edge factor specified.

Frog: Filter Size 9×9

Mean Filter Blurring

A Mean Filter Blur, also known as a Box Blur, can be performed through image convolution. The size of the matrix/kernel implemented when preforming image convolution will be determined through user input.

Every matrix/kernel element should be set to one. The resulting value should be multiplied by a factor value equating to one divided by the matrix/kernel size. As an example, a matrix/kernel size of 3×3 can be expressed as follows:

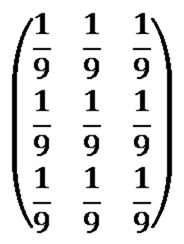
An alternative expression can also be:

Frog: Filter Size 9×9

Boolean Edge Detection without a local threshold

When performing Boolean Edge Detection a local threshold should be implemented in order to exclude image noise. In this article we rely on the interference of image noise in order to render a fuzzy image effect. By not implementing a local threshold when performing Boolean Edge detection the sample source code ensures sufficient interference from image noise.

The steps involved in performing Boolean Edge Detection without a local threshold can be described as follows:

Calculate Neighbourhood Mean – Iterate each pixel forming part of the source/input image. Using a 3×3 matrix size calculate the mean value of the neighbourhood surrounding the pixel currently being iterated.
Create Mean comparison Matrix – Once again using a 3×3 matrix size compare each neighbourhood pixel to the newly calculated mean value. Create a temporary 3×3 size matrix, each matrix element’s value should be the result of mean comparison. Should the value expressed by a neighbourhood pixel exceed the mean value the corresponding temporary matrix element should be set to one. When the calculated mean value exceeds the value of a neighbourhood pixel the corresponding temporary matrix element should be set to zero.
Compare Edge Masks – Using sixteen predefined edge masks compare the temporary matrix created in the previous step to each edge mask. If the temporary matrix matches one of the predefined edge masks multiply the specified factor to the pixel currently being iterated.

Note: A detailed article on Boolean Edge detection implementing a local threshold can be found here: C# How to: Boolean Edge Detection

Frog: Filter Size 9×9

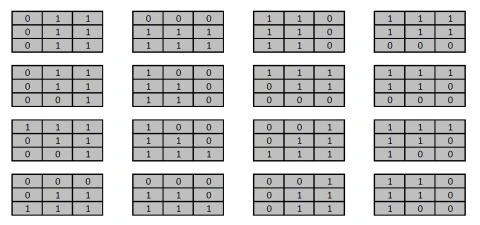
The sixteen predefined edge masks each represent an image edge in a different direction. The predefined edge masks can be expressed as:

Frog: Filter Size 13×13

Implementing a Mean Filter

The sample source code defines the MeanFilter method, an extension method targeting the Bitmap class. The definition listed as follows:

private static Bitmap MeanFilter(this Bitmap sourceBitmap, 
                                 int meanSize)
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length];


    double blue = 0.0, green = 0.0, red = 0.0;
    double factor = 1.0 / (meanSize * meanSize);


    int imageStride = sourceBitmap.Width * 4;
    int filterOffset = meanSize / 2; 
    int calcOffset = 0, filterY = 0, filterX = 0; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4)
    {
        blue = 0; green = 0; red = 0;
        filterY = -filterOffset;
        filterX = -filterOffset;


        while (filterY <= filterOffset)
        {
            calcOffset = k + (filterX * 4) +
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 :
            (calcOffset >= pixelBuffer.Length - 2 ?
            pixelBuffer.Length - 3 : calcOffset));


            blue += pixelBuffer[calcOffset];
            green += pixelBuffer[calcOffset + 1];
            red += pixelBuffer[calcOffset + 2];


            filterX++;


            if (filterX > filterOffset)
            {
                filterX = -filterOffset;
                filterY++;
            }
        }


        resultBuffer[k] = ClipByte(factor * blue);
        resultBuffer[k + 1] = ClipByte(factor * green);
        resultBuffer[k + 2] = ClipByte(factor * red);
        resultBuffer[k + 3] = 255;
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height);
}

Frog: Filter Size 19×19

Implementing Boolean Edge Detection

Boolean Edge detection is performed in the sample source code through the implementation of the BooleanEdgeDetectionFilter method. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the BooleanEdgeDetectionFilter extension method:

public static Bitmap BooleanEdgeDetectionFilter( 
       this Bitmap sourceBitmap, float edgeFactor) 
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length]; 
    Buffer.BlockCopy(pixelBuffer, 0, resultBuffer, 
                     0, pixelBuffer.Length); 


    List<string> edgeMasks = GetBooleanEdgeMasks(); 
 
    int imageStride = sourceBitmap.Width * 4; 
    int matrixMean = 0, pixelTotal = 0; 
    int filterY = 0, filterX = 0, calcOffset = 0; 
    string matrixPatern = String.Empty; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    {
        matrixPatern = String.Empty; 
        matrixMean = 0; pixelTotal = 0; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 
 
            matrixMean += pixelBuffer[calcOffset]; 
            matrixMean += pixelBuffer[calcOffset + 1]; 
            matrixMean += pixelBuffer[calcOffset + 2]; 


            filterX += 1; 


            if (filterX > 1) 
             { filterX = -1; filterY += 1; } 
        }


        matrixMean = matrixMean / 9; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 


            pixelTotal = pixelBuffer[calcOffset]; 
            pixelTotal += pixelBuffer[calcOffset + 1]; 
            pixelTotal += pixelBuffer[calcOffset + 2]; 
 
            matrixPatern += (pixelTotal > matrixMean 
                                       ? "1" : "0"); 
            filterX += 1; 


            if (filterX > 1) 
            { filterX = -1; filterY += 1; } 
        } 


        if (edgeMasks.Contains(matrixPatern)) 
        {
            resultBuffer[k] = 
            ClipByte(resultBuffer[k] * edgeFactor); 


            resultBuffer[k + 1] = 
            ClipByte(resultBuffer[k + 1] * edgeFactor); 


            resultBuffer[k + 2] = 
            ClipByte(resultBuffer[k + 2] * edgeFactor); 
        }
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height); 
}

Frog: Filter Size 13×13

The predefined edge masks implemented in mean comparison have been wrapped by the GetBooleanEdgeMasks method. The definition as follows:

public static List<string> GetBooleanEdgeMasks() 
{
    List<string> edgeMasks = new List<string>(); 


    edgeMasks.Add("011011011"); 
    edgeMasks.Add("000111111"); 
    edgeMasks.Add("110110110"); 
    edgeMasks.Add("111111000"); 
    edgeMasks.Add("011011001"); 
    edgeMasks.Add("100110110"); 
    edgeMasks.Add("111011000"); 
    edgeMasks.Add("111110000"); 
    edgeMasks.Add("111011001"); 
    edgeMasks.Add("100110111"); 
    edgeMasks.Add("001011111"); 
    edgeMasks.Add("111110100"); 
    edgeMasks.Add("000011111"); 
    edgeMasks.Add("000110111"); 
    edgeMasks.Add("001011011"); 
    edgeMasks.Add("110110100"); 


    return edgeMasks; 
}

Frog: Filter Size 19×19

Implementing a Fuzzy Blur Filter

The FuzzyEdgeBlurFilter method serves as the implementation of a Fuzzy Blur Filter. As discussed earlier a Fuzzy Blur Filter involves enhancing image edges through Boolean Edge detection, performing a Mean Filter blur and then once again performing Boolean Edge detection. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the FuzzyEdgeBlurFilter method:

public static Bitmap FuzzyEdgeBlurFilter(this Bitmap sourceBitmap,  
                                         int filterSize,  
                                         float edgeFactor1,  
                                         float edgeFactor2) 
{
    return  
    sourceBitmap.BooleanEdgeDetectionFilter(edgeFactor1). 
    MeanFilter(filterSize).BooleanEdgeDetectionFilter(edgeFactor2); 
}

Frog: Filter Size 3×3

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Tyler’s Tree Frog
Attribution: LiquidGhoul. This file has been released into the public domain by its author, LiquidGhoul. This applies worldwide.
Download from Wikipedia.

Phyllobates Terribilis
Attribution: Wilfried Berns. This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Germany license.
Download from Wikipedia.

Dendropsophus Microcephalus
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia

Panamanian Golden Frog
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia.

C# How to: Image Boundary Extraction

Published July 21, 2013 Augmented Reality , Blogging , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Arithmetic , Image Filters , Image Processing , Image Transform , Learn Everyday , Microsoft , Morphology Filters , New Version , Opensource , Tip , Update 5 Comments
Tags: Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Boundary Sharpen, Boundary Tracing, C#, Code Sample, Computer vision, Converting Images, Edge Detect, Edge Detection, Edge enhance, Edge Tracing, Feature extraction, Graphic Filters, Image, Image Boundary Extraction, Image Difference, Image Dilation, Image Erosion, Image Intensity, Image Morphology, Image processing, Image Sharpen, Image Transform, Machine vision, Morphologial Filters, Morphological Edge Detection, Morphological Transform, Pixel Filters, Structured Element

Article Purpose

This article explores various image processing concepts, which feature in combination when implementing Image Boundary Extraction. Concepts covered within this article include: Morphological Image Erosion and Image Dilation, Image Addition and Subtraction, Boundary Sharpening, Boundary Tracing and Boundary Extraction.

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article’s accompanying sample source code includes the definition of a sample application. The sample application serves as an implementation of the concepts discussed in this article. In using the sample application concepts can be easily tested and replicated.

The sample application has been defined as a Windows Forms application. The user interface enables the user to configure several options which influence the output produced from image filtering processes. The following section describes the options available to a user when executing the sample application:

Loading and Saving files – Users can specify source/input images through clicking the Load Image button. If desired, resulting filtered images can be saved to the local file system when clicking the Save Image button.
Filter Type – The types of filters implemented represent variations on Image Boundary Extraction. The supported filter types are: Conventional Boundary extraction, Boundary Sharpening and Boundary Tracing.
Filter Size – Filter intensity/strength will mostly be reliant on the filter size implemented. A Filter size represents the number of neighbouring pixels examined when applying filters.
Colours Applied – The sample source code and sample application provides functionality allowing a filter to only effect user specified colour components. Colour components are represented in the form of an RGB colour scheme. The inclusion or exclusion of the colour components Red, Green and Blue will be determined through user configuration.
Structuring Element – As mentioned, the Filter Size option determines the size of neighbourhood pixels examined. The Structuring Element’s setup determine the neighbouring pixels within the pixel neighbourhood size bounds that should be used as input when calculating filter results.

The following image is a screenshot of the Image Boundary Extraction sample application in action:

Parrot: Boundary Extraction, 3×3, Green

Morphological Boundary Extraction

Image Boundary Extraction can be considered a method of Image Edge Detection. In contrast to more commonly implemented gradient based edge detection methods, Image Boundary Extraction originates from Morphological Image Filters.

When drawing a comparison, Image Boundary Extraction and Morphological Edge Detection express strong similarities. Morphological Edge Detection results from the difference in image erosion and image dilation. Considered from a different point of view, creating one image expressing thicker edges and another image expressing thinner edges provides the means to calculate the difference in edges.

Image Boundary Extraction implements the same concept as Morphological Edge Detection. The base concept can be regarded as calculating the difference between two images which rendered the same image, but expressing a difference in image edges. Image Boundary Extraction relies on calculating the difference between either image erosion and the source image or image dilation and the source image. The difference between image erosion and image dilation in most cases result in more of difference than the difference between image erosion and the source image or image dilation and the source image. The result of Image Boundary Extraction representing less of a difference than Morphological Edge Detection can be observed in Image Boundary Extraction being expressed in finer/smaller width lines.

Difference of Gaussians is another method of edge detection which functions along the same basis. Edges are determined by calculating the difference between two images, each having been filtered from the same source image, using a Gaussian blur of differing intensity levels.

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Boundary Sharpening

The concept of Boundary Sharpening refers to enhancing or sharpening the boundaries or edges expressed in a source/input image. Boundaries can be easily determined or extracted as discussed earlier when exploring Boundary Extraction.

The steps involved in performing Boundary Sharpening can be described as follows:

Extract Boundaries – Determine boundaries by performing image dilation and calculating the difference between the dilated image and the source image.
Match Source Edges and Extracted Boundaries – The boundaries extracted in the previous step represent the difference between image dilation and the original source image. Ensure that extracted boundaries match the source image through performing image dilation on a copy of the source/input image.
Emphasise Extracted boundaries in source image – Perform image addition using the extracted boundaries image and dilated copy of the source image.

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Boundary Tracing

Boundary Tracing refers to applying image filters which result in image edges/boundaries appearing darker or more pronounced. This type of filter also relies on Boundary Extraction.

Boundary Tracing can be implemented in two steps, described as follows:

Extract Boundaries – Determine boundaries by performing image dilation and calculating the difference between the dilated image and the source image.
Emphasise Extracted boundaries in source image – Subtract the extracted boundaries from the original source image.

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Implementing Morphological Erosion and Dilation

The accompanying sample source code defines the MorphologyOperation method, defined as an extension method targeting the Bitmap class. In terms of parameters this method expects a two dimensional array representing a structuring element. The other required parameter represents an enumeration value indicating which Morphological Operation to perform, either erosion or dilation.

The following code snippet provides the definition in full:

private static Bitmap MorphologyOperation(this Bitmap sourceBitmap,
                                          bool[,] se,
                                          MorphologyOperationType morphType,
                                          bool applyBlue = true,
                                          bool applyGreen = true,
                                          bool applyRed = true)
{ 
    BitmapData sourceData =
               sourceBitmap.LockBits(new Rectangle(0, 0,
               sourceBitmap.Width, sourceBitmap.Height),
               ImageLockMode.ReadOnly,
               PixelFormat.Format32bppArgb);


    byte[] pixelBuffer = new byte[sourceData.Stride *
                                  sourceData.Height];


    byte[] resultBuffer = new byte[sourceData.Stride *
                                   sourceData.Height];


    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,
                               pixelBuffer.Length);


    sourceBitmap.UnlockBits(sourceData);


    int filterOffset = (se.GetLength(0) - 1) / 2;
    int calcOffset = 0, byteOffset = 0;
    byte blueErode = 0, greenErode = 0, redErode = 0;
    byte blueDilate = 0, greenDilate = 0, redDilate = 0;


    for (int offsetY = 0; offsetY <
        sourceBitmap.Height - filterOffset; offsetY++)
    {
        for (int offsetX = 0; offsetX <
            sourceBitmap.Width - filterOffset; offsetX++)
        {
            byteOffset = offsetY * sourceData.Stride +
                         offsetX * 4;


            blueErode = 255; greenErode = 255; redErode = 255;
            blueDilate = 0; greenDilate = 0; redDilate = 0;


            for (int filterY = -filterOffset;
                    filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
                {
                    if (se[filterY + filterOffset,  
                           filterX + filterOffset] == true)
                    {
                        calcOffset = byteOffset +
                                     (filterX * 4) +
                        (filterY * sourceData.Stride);


                        calcOffset = (calcOffset < 0 ? 0 :
                        (calcOffset >= pixelBuffer.Length + 2 ?
                        pixelBuffer.Length - 3 : calcOffset));


                        blueDilate =  
                        (pixelBuffer[calcOffset] > blueDilate ?
                        pixelBuffer[calcOffset] : blueDilate);


                        greenDilate =  
                        (pixelBuffer[calcOffset + 1] > greenDilate ?
                        pixelBuffer[calcOffset + 1] : greenDilate);


                        redDilate =  
                        (pixelBuffer[calcOffset + 2] > redDilate ?
                        pixelBuffer[calcOffset + 2] : redDilate);


                        blueErode =  
                        (pixelBuffer[calcOffset] < blueErode ?
                        pixelBuffer[calcOffset] : blueErode);


                        greenErode =  
                        (pixelBuffer[calcOffset + 1] < greenErode ?
                        pixelBuffer[calcOffset + 1] : greenErode);


                        redErode =  
                        (pixelBuffer[calcOffset + 2] < redErode ?
                        pixelBuffer[calcOffset + 2] : redErode);
                    }
                }
            }


            blueErode = (applyBlue ? blueErode : pixelBuffer[byteOffset]);
            blueDilate = (applyBlue ? blueDilate : pixelBuffer[byteOffset]);


            greenErode = (applyGreen ? greenErode : pixelBuffer[byteOffset + 1]);
            greenDilate = (applyGreen ? greenDilate : pixelBuffer[byteOffset + 1]);


            redErode = (applyRed ? redErode : pixelBuffer[byteOffset + 2]);
            redDilate = (applyRed ? redDilate : pixelBuffer[byteOffset + 2]);


            if (morphType == MorphologyOperationType.Erosion)
            {
                resultBuffer[byteOffset] = blueErode;
                resultBuffer[byteOffset + 1] = greenErode;
                resultBuffer[byteOffset + 2] = redErode;
            }
            else if (morphType == MorphologyOperationType.Dilation)
            {
                resultBuffer[byteOffset] = blueDilate;
                resultBuffer[byteOffset + 1] = greenDilate;
                resultBuffer[byteOffset + 2] = redDilate;
            }


            resultBuffer[byteOffset + 3] = 255;
        }
    }


    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height);
    BitmapData resultData = resultBitmap.LockBits(new Rectangle(0, 0,
                            resultBitmap.Width, resultBitmap.Height),
                            ImageLockMode.WriteOnly,
                            PixelFormat.Format32bppArgb);


    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);


    resultBitmap.UnlockBits(resultData);


    return resultBitmap;
}

Parrot: Boundary Extraction, 3×3, Red, Green

Implementing Image Addition

The sample source code encapsulates the process of combining two separate images through means of addition. The AddImage method serves as a single declaration of image addition functionality. This method has been defined as an extension method targeting the Bitmap class. Boundary Sharpen filtering implements image addition.

The following code snippet provides the definition of the AddImage extension method:

private static Bitmap AddImage(this Bitmapsource Bitmap, 
                               Bitmap addBitmap)
{
    BitmapData sourceData =
               sourceBitmap.LockBits(new Rectangle (0, 0,
               sourceBitmap.Width, sourceBitmap.Height),
               ImageLockMode.ReadOnly,
               PixelFormat.Format32bppArgb);


    byte[] resultBuffer = new byte[sourceData.Stride *
                                  sourceData.Height];


    Marshal.Copy(sourceData.Scan0, resultBuffer, 0,
                               resultBuffer.Length);


    sourceBitmap.UnlockBits(sourceData);


    BitmapData addData =
               addBitmap.LockBits(new Rectangle(0, 0,
               addBitmap.Width, addBitmap.Height),
               ImageLockMode.ReadOnly,
               PixelFormat.Format32bppArgb);


    byte[] addBuffer = new byte[addData.Stride *
                                  addData.Height];


    Marshal.Copy(addData.Scan0, addBuffer, 0,
                               addBuffer.Length);


    addBitmap.UnlockBits(addData);


    for (int k = 0; k + 4 < resultBuffer.Length &&
                    k + 4 < addBuffer.Length; k += 4)
    {
        resultBuffer[k] =
        AddColors(resultBuffer[k], addBuffer[k]);
 
        resultBuffer[k + 1] =
        AddColors(resultBuffer[k + 1], addBuffer[k + 1]);
 
        resultBuffer[k + 2] =
        AddColors(resultBuffer[k + 2], addBuffer[k + 2]);
 
        resultBuffer[k + 3] = 255;
    }


    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
                                     sourceBitmap.Height);


    BitmapData resultData =
               resultBitmap.LockBits(new Rectangle(0, 0,
               resultBitmap.Width, resultBitmap.Height),
               ImageLockMode.WriteOnly,
               PixelFormat.Format32bppArgb);


    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);


    resultBitmap.UnlockBits(resultData);


    return resultBitmap;
}

private static byte AddColors(byte color1, byte color2) 
{
    int result = color1 + color2; 

 
    return (byte)(result < 0 ? 0 : (result > 255 ? 255 : result)); 
}

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Implementing Image Subtraction

In a similar fashion regarding the AddImage method the sample code defines the SubractImage method. By definition this method serves as an extension method targeting the Bitmap class. Image subtraction has been implemented in Boundary Extraction and Boundary Tracing.

The definition of the SubtractImage method listed as follows:

private static Bitmap SubtractImage(this Bitmap sourceBitmap,  
                                         Bitmap subtractBitmap) 
{
    BitmapData sourceData = 
               sourceBitmap.LockBits(new Rectangle(0, 0, 
               sourceBitmap.Width, sourceBitmap.Height), 
               ImageLockMode.ReadOnly, 
               PixelFormat.Format32bppArgb); 


    byte[] resultBuffer = new byte[sourceData.Stride * 
                                  sourceData.Height]; 


    Marshal.Copy(sourceData.Scan0, resultBuffer, 0, 
                               resultBuffer.Length); 


    sourceBitmap.UnlockBits(sourceData); 


    BitmapData subtractData = 
               subtractBitmap.LockBits(new Rectangle(0, 0, 
               subtractBitmap.Width, subtractBitmap.Height), 
               ImageLockMode.ReadOnly, 
               PixelFormat.Format32bppArgb); 


    byte[] subtractBuffer = new byte[subtractData.Stride * 
                                  subtractData.Height]; 


    Marshal.Copy(subtractData.Scan0, subtractBuffer, 0, 
                               subtractBuffer.Length); 


    subtractBitmap.UnlockBits(subtractData); 


    for (int  k = 0; k + 4 < resultBuffer.Length &&  
                    k + 4 < subtractBuffer.Length; k += 4) 
    { 
        resultBuffer[k] =  
        SubtractColors(resultBuffer[k], subtractBuffer[k]); 


        resultBuffer[k + 1] =  
        SubtractColors(resultBuffer[k + 1], subtractBuffer[k + 1]); 


        resultBuffer[k + 2] = 
        SubtractColors(resultBuffer[k + 2], subtractBuffer[k + 2]); 


        resultBuffer[k + 3] = 255; 
    }


    Bitmap resultBitmap = new Bitmap (sourceBitmap.Width, 
                                     sourceBitmap.Height); 


    BitmapData resultData = 
               resultBitmap.LockBits(new Rectangle (0, 0, 
               resultBitmap.Width, resultBitmap.Height), 
               ImageLockMode.WriteOnly, 
               PixelFormat.Format32bppArgb); 


    Marshal.Copy(resultBuffer, 0, resultData.Scan0, 
                               resultBuffer.Length); 


    resultBitmap.UnlockBits(resultData); 


    return resultBitmap; 
}

private static byte SubtractColors(byte color1, byte color2) 
{
    int result = (int)color1 - (int)color2; 

 
    return (byte)(result < 0 ? 0 : result); 
}

Parrot: Boundary Extraction, 3×3, Green

Implementing Image Boundary Extraction

In the sample source code processing Image Boundary Extraction can be achieved when invoking the BoundaryExtraction method. Defined as an extension method, the BoundaryExtraction method targets the Bitmap class.

As discussed earlier, this method performs Boundary Extraction through subtracting the source image from a dilated copy of the source image.

The following code snippet details the definition of the BoundaryExtraction method:

private static Bitmap
BoundaryExtraction(this Bitmap sourceBitmap, 
                   bool[,] se, bool applyBlue = true, 
                   bool applyGreen = true, bool applyRed = true) 
{
    Bitmap resultBitmap = 
           sourceBitmap.MorphologyOperation(se,  
           MorphologyOperationType.Dilation, applyBlue,  
                                  applyGreen, applyRed); 

 
    resultBitmap = resultBitmap.SubtractImage(sourceBitmap); 

  
    return resultBitmap; 
}

Parrot: Boundary Extraction, 3×3, Red, Blue

Implementing Image Boundary Sharpening

Boundary Sharpening in the sample source code has been implemented through the definition of the BoundarySharpen method. The BoundarySharpen extension method targets the Bitmap class. The following code snippet provides the definition:

private static Bitmap 
BoundarySharpen(this Bitmap sourceBitmap, 
                bool[,] se, bool applyBlue = true, 
                bool applyGreen = true, bool applyRed = true) 
{
    Bitmap resultBitmap = 
           sourceBitmap.BoundaryExtraction(se, applyBlue, 
                                           applyGreen, applyRed); 


    resultBitmap = sourceBitmap.MorphologyOperation(se,  
                   MorphologyOperationType.Dilation, applyBlue,  
                   applyGreen, applyRed).AddImage(resultBitmap); 


    return resultBitmap; 
}

Parrot: Boundary Extraction, 3×3, Green

Implementing Image Boundary Tracing

Boundary Tracing has been defined through the BoundaryTrace extension method, which targets the Bitmap class. Similar to the BoundarySharpen method this method performs Boundary Extraction, the result of which serves to be subtracted from the original source image. Subtracting image boundaries/edges result in those boundaries/edges being darkened, or traced. The definition of the BoundaryTracing extension method detailed as follows:

private static Bitmap
BoundaryTrace(this Bitmap sourceBitmap, 
              bool[,] se, bool applyBlue = true, 
              bool applyGreen = true, bool applyRed = true) 
{
    Bitmap resultBitmap =
    sourceBitmap.BoundaryExtraction(se, applyBlue,  
                                    applyGreen, applyRed); 


    resultBitmap = sourceBitmap.SubtractImage(resultBitmap); 

 
    return resultBitmap; 
}

Parrot: Boundary Extraction, 3×3, Green, Blue

Implementing a Wrapper Method

The BoundaryExtractionFilter method is the only method defined as publicly accessible. Following convention, this method’s definition signals the method as an extension method targeting the Bitmap class. This method has the intention of acting as a wrapper method, a single method capable of performing Boundary Extraction, Boundary Sharpening and Boundary Tracing, depending on method parameters.

The definition of the BoundaryExtractionFilter method detailed by the following code snippet:

public static Bitmap
BoundaryExtractionFilter(this Bitmap sourceBitmap, 
                         bool[,] se, BoundaryExtractionFilterType  
                         filterType, bool applyBlue = true, 
                         bool applyGreen = true, bool applyRed = true) 
{
    Bitmap resultBitmap = null; 

 
    if (filterType == BoundaryExtractionFilterType.BoundaryExtraction) 
    {
        resultBitmap =  
        sourceBitmap.BoundaryExtraction(se, applyBlue, 
                                        applyGreen, applyRed); 
    }
    else if (filterType == BoundaryExtractionFilterType.BoundarySharpen) 
    {
        resultBitmap =  
        sourceBitmap.BoundarySharpen(se, applyBlue,  
                                     applyGreen, applyRed); 
    }
    else if (filterType == BoundaryExtractionFilterType.BoundaryTrace) 
    {
        resultBitmap =  
        sourceBitmap.BoundaryTrace(se, applyBlue,  
                                   applyGreen, applyRed); 
    }

 
    return resultBitmap; 
}

Parrot: Boundary Extraction, 3×3, Red, Green, Blue

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Scarlet Macaw at Diergaarde Blijdorp, Rotterdam, Netherlands.
Attributed to: Jar0d. This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license.
Download from Wikipedia

A Scarlet Macaw flying away from the photographer.
Attributed to: Robert01. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Germany license.
Download from Wikipedia

Blue-and-yellow Macaw in flight.
Attributed to: Luc Viatour – www.lucnix.be. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia

Two Green-winged Macaws (also known as the Red-and-green Macaw) resting at Seaport Village, San Diego, USA.
Attributed to: Dave Fayram. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikimedia.org

A Scarlet Macaw riding a small tricycle at an exhibition in Spain.
Attributed to: The Torch. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia.

Long-tailed Broadbill (Psarisomus dalhousiae), Kaeng Krachan National Park, Phetchaburi, Thailand.
Attributed to User-JJ Harrison. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia.

C# How to: Image Unsharp Mask

Published May 18, 2013 Augmented Reality , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , Opensource , Tip 32 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, BitmapData.Stride, C#, C# Convolution, Code Sample, Computer vision, Convolution filters, Convolution Kernel, Convolution matrix, Edge enhance, Extension Methods, Feature extraction, Gaussian, Gaussian Blur, Graphic Filters, Image Blur, Image processing, Image Sharpness, Image Transform, Machine vision, Matrix, Mean Filter, Pixel Filters, Pixel Manipulation, Unsharp, Unsharp Masking

Article purpose

The purpose of this article is to explore and illustrate the concept of Image Unsharp Masking. This article implements image convolution in the form of a 3×3 Gaussian Blur, 5×5 Gaussian Blur, 3×3 Mean filter and a 5×5 Mean filter.

Sample Source code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample source code associated with this article includes a Windows Forms based sample application implementing the concepts explored throughout this article.

When using the Image Unsharp Mask sample application users can select a source/input image from the local file system by clicking the Load Image button. The dropdown combobox at the bottom of the screen allows the user to select an unsharp masking variation. On the right hand side of the screen users can specify the level/intensity of resulting image sharpness.

Clicking the Save Image button allows a user to save resulting images to the local file system. The image below is a screenshot of the Image Unsharp Mask sample application in action:

What is Image Unsharp Masking?

A good definition of Image Unsharp Masking can be found on Wikipedia:

Unsharp masking (USM) is an image manipulation technique, often available in digital image processing software.

The "unsharp" of the name derives from the fact that the technique uses a blurred, or "unsharp", positive image to create a "mask" of the original image. The unsharped mask is then combined with the negative image, creating an image that is less blurry than the original. The resulting image, although clearer, probably loses accuracy with respect to the image’s subject. In the context of signal-processing, an unsharp mask is generally a linear or nonlinear filter that amplifies high-frequency components.

In this article we implement Image Unsharp Masking by first creating a blurred copy of a source/input image then subtracting the blurred image from the original image, which is known as the mask. Increased image sharpness is achieved by adding a factor of the mask to the original image.

Applying a Convolution Matrix filter

The sample source code provides the definition for the ConvolutionFilter extension method targeting the Bitmap class. This method is invoked when implementing image blurring. The definition of the ConvolutionFilter extension method as follows:

 private static Bitmap ConvolutionFilter(Bitmap sourceBitmap,  
                                     double[,] filterMatrix,  
                                          double factor = 1,  
                                               int bias = 0,  
                                     bool grayscale = false )  
{ 
     BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0, 
                              sourceBitmap.Width, sourceBitmap.Height), 
                                                ImageLockMode.ReadOnly,  
                                          PixelFormat.Format32bppArgb); 

  
     byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
     byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

  
     Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
     sourceBitmap.UnlockBits(sourceData); 

  
     if (grayscale == true) 
     {
         float rgb = 0; 

  
         for (int k = 0; k < pixelBuffer.Length; k += 4) 
         { 
             rgb = pixelBuffer[k] * 0.11f; 
             rgb += pixelBuffer[k + 1] * 0.59f; 
             rgb += pixelBuffer[k + 2] * 0.3f; 

  
             pixelBuffer[k] = (byte )rgb; 
             pixelBuffer[k + 1] = pixelBuffer[k]; 
             pixelBuffer[k + 2] = pixelBuffer[k]; 
             pixelBuffer[k + 3] = 255; 
         } 
     } 

  
     double blue = 0.0; 
     double green = 0.0; 
     double red = 0.0; 

  
     int filterWidth = filterMatrix.GetLength(1); 
     int filterHeight = filterMatrix.GetLength(0); 

  
     int filterOffset = (filterWidth-1) / 2; 
     int calcOffset = 0; 

  
     int byteOffset = 0; 

  
     for (int offsetY = filterOffset; offsetY <  
         sourceBitmap.Height - filterOffset; offsetY++) 
     { 
         for (int  offsetX = filterOffset; offsetX <  
             sourceBitmap.Width - filterOffset; offsetX++) 
         { 
             blue = 0; 
             green = 0; 
             red = 0; 

  
             byteOffset = offsetY *  
                          sourceData.Stride +  
                          offsetX * 4; 

   
             for (int  filterY = -filterOffset;  
                 filterY <= filterOffset; filterY++) 
             {
                 for (int  filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                 { 

   
                     calcOffset = byteOffset +  
                                  (filterX * 4) +  
                                  (filterY * sourceData.Stride); 

  
                     blue += (double)(pixelBuffer[calcOffset]) * 
                             filterMatrix[filterY + filterOffset,  
                                          filterX + filterOffset]; 

  
                     green += (double)(pixelBuffer[calcOffset + 1]) * 
                              filterMatrix[filterY + filterOffset,  
                                           filterX + filterOffset]; 

   
                     red += (double)(pixelBuffer[calcOffset + 2]) * 
                            filterMatrix[filterY + filterOffset,  
                                         filterX + filterOffset]; 
                 }
             }

   
             blue = factor * blue + bias; 
             green = factor * green + bias; 
             red = factor * red + bias; 

  
             if (blue > 255) 
             { blue = 255; } 
             else if (blue < 0) 
             { blue = 0; } 

  
             if (green > 255) 
             { green = 255; } 
             else if (green < 0) 
             { green = 0; } 

  
             if (red > 255) 
             { red = 255; } 
             else if (red < 0) 
             { red = 0; } 

  
             resultBuffer[byteOffset] = (byte )(blue); 
             resultBuffer[byteOffset + 1] = (byte )(green); 
             resultBuffer[byteOffset + 2] = (byte )(red); 
             resultBuffer[byteOffset + 3] = 255; 
        }
    } 

  
     Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
                                      sourceBitmap.Height); 
  
     BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                              resultBitmap.Width, resultBitmap.Height), 
                                               ImageLockMode.WriteOnly, 
                                          PixelFormat.Format32bppArgb); 

  
     Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
     resultBitmap.UnlockBits(resultData); 

   
     return resultBitmap; 
}

Subtracting and Adding Images

An important step required when implementing Image Unsharp Masking comes in the form of creating a mask by subtracting a blurred copy from the original image and then adding a factor of the mask to the original image. In order to achieve increased performance the sample source code combines the process of creating the mask and adding the mask to the original image.

The SubtractAddFactorImage extension method iterates every pixel that forms part of an image. In a single step the blurred pixel is subtracted from the original pixel, multiplied by a user specified factor and then added to the original pixel. The definition of the SubtractAddFactorImage extension method as follows:

private static Bitmap SubtractAddFactorImage( 
                              this Bitmap subtractFrom, 
                                  Bitmap subtractValue, 
                                   float factor = 1.0f) 
{ 
    BitmapData sourceData =  
               subtractFrom.LockBits(new Rectangle (0, 0, 
               subtractFrom.Width, subtractFrom.Height), 
               ImageLockMode.ReadOnly, 
               PixelFormat.Format32bppArgb); 

  
    byte[] sourceBuffer = new byte[sourceData.Stride *  
                                   sourceData.Height]; 

  
    Marshal.Copy(sourceData.Scan0, sourceBuffer, 0,  
                                sourceBuffer.Length); 

  
    byte[] resultBuffer = new byte[sourceData.Stride *  
                                   sourceData.Height]; 

  
    BitmapData subtractData =  
               subtractValue.LockBits(new Rectangle (0, 0, 
               subtractValue.Width, subtractValue.Height), 
               ImageLockMode.ReadOnly, 
               PixelFormat.Format32bppArgb); 

  
    byte[] subtractBuffer = new byte[subtractData.Stride * 
                                     subtractData.Height]; 

  
    Marshal.Copy(subtractData.Scan0, subtractBuffer, 0, 
                                 subtractBuffer.Length); 

  
    subtractFrom.UnlockBits(sourceData); 
    subtractValue.UnlockBits(subtractData); 

  
    double blue = 0; 
    double green = 0; 
    double red = 0; 

  
    for (int k = 0; k < resultBuffer.Length && 
                   k < subtractBuffer.Length; k += 4) 
    { 
        blue = sourceBuffer[k] +  
              (sourceBuffer[k] - 
               subtractBuffer[k]) * factor; 

  
        green = sourceBuffer[k + 1] +  
               (sourceBuffer[k + 1] - 
                subtractBuffer[k + 1]) * factor; 

  
        red = sourceBuffer[k + 2] +  
             (sourceBuffer[k + 2] - 
              subtractBuffer[k + 2]) * factor; 

  
        blue = (blue < 0 ? 0 : (blue > 255 ? 255 : blue)); 
        green = (green < 0 ? 0 : (green > 255 ? 255 : green)); 
        red = (red < 0 ? 0 : (red > 255 ? 255 : red)); 

  
        resultBuffer[k] = (byte )blue; 
        resultBuffer[k + 1] = (byte )green; 
        resultBuffer[k + 2] = (byte )red; 
        resultBuffer[k + 3] = 255; 
    }

  
    Bitmap resultBitmap = new Bitmap (subtractFrom.Width,  
                                     subtractFrom.Height); 

  
    BitmapData resultData =  
               resultBitmap.LockBits(new Rectangle (0, 0, 
               resultBitmap.Width, resultBitmap.Height), 
               ImageLockMode.WriteOnly, 
               PixelFormat.Format32bppArgb); 

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,  
                               resultBuffer.Length); 

  
    resultBitmap.UnlockBits(resultData); 

  
    return resultBitmap; 
}

Matrix Definition

The image blurring convolution filters implemented by the sample source code relies on static matrix/kernel values defined in the Matrix class. The variants of blurring implemented are: 3×3 Gaussian, 5×5 Gaussian, 3×3 Mean and 5×5 Mean. The definition of the Matrix class is detailed by the following code snippet:

public static class Matrix
{
    public static double[,] Gaussian3x3
    {
        get
        {
            return new double[,]
            { { 1, 2, 1, }, 
              { 2, 4, 2, }, 
              { 1, 2, 1, }, };
        }
    }

  
    public static double[,] Gaussian5x5Type1
    {
        get
        {
            return new double[,]
            { { 2, 04, 05, 04, 2 }, 
              { 4, 09, 12, 09, 4 },
              { 5, 12, 15, 12, 5 },
              { 4, 09, 12, 09, 4 },
              { 2, 04, 05, 04, 2 }, };
        }
    }

  
    public static double[,] Mean3x3
    {
        get
        {
            return new double[,]
            { { 1, 1, 1, }, 
              { 1, 1, 1, }, 
              { 1, 1, 1, }, };
        }
    }

  
    public static double[,] Mean5x5
    {
        get
        {
            return new double[,]
            { { 1, 1, 1, 1, 1 }, 
              { 1, 1, 1, 1, 1 },
              { 1, 1, 1, 1, 1 },
              { 1, 1, 1, 1, 1 },
              { 1, 1, 1, 1, 1 }, };
        }
    }
}

Implementing Image Unsharpening

This article explores four variants of Image Unsharp Masking, relating to the four types of image blurring discussed in the previous section. The sample source code defines the following Image Unsharp Masking extension methods: UnsharpGaussian3x3, UnsharpGaussian5x5, UnsharpMean3x3 and UnsharpMean5x5. All four methods are defined as extension methods targeting the Bitmap class. When looking at the sample images in the following section you will notice the correlation between increased image blurring and enhanced image sharpness. The definition as follows:

public static Bitmap UnsharpGaussian3x3( 
                                 this Bitmap sourceBitmap,  
                                 float factor = 1.0f) 
{
    Bitmap blurBitmap = ExtBitmap.ConvolutionFilter( 
                                  sourceBitmap,  
                                  Matrix.Gaussian3x3,  
                                  1.0 / 16.0); 

   
    Bitmap resultBitmap =  
           sourceBitmap.SubtractAddFactorImage( 
                        blurBitmap, factor); 

   
    return resultBitmap; 
 } 

   
public static Bitmap UnsharpGaussian5x5( 
                                 this Bitmap sourceBitmap, 
                                 float factor = 1.0f) 
{
    Bitmap blurBitmap = ExtBitmap.ConvolutionFilter( 
                                  sourceBitmap,  
                                  Matrix.Gaussian5x5Type1,  
                                  1.0 / 159.0); 

   
    Bitmap resultBitmap = 
           sourceBitmap.SubtractAddFactorImage( 
                        blurBitmap, factor); 

   
    return resultBitmap; 
} 
 
public static Bitmap UnsharpMean3x3( 
                                 this Bitmap sourceBitmap, 
                                 float factor = 1.0f) 
{ 
    Bitmap blurBitmap = ExtBitmap.ConvolutionFilter( 
                                  sourceBitmap,  
                                  Matrix.Mean3x3,  
                                  1.0 / 9.0); 

   
    Bitmap resultBitmap = 
           sourceBitmap.SubtractAddFactorImage( 
                        blurBitmap, factor); 

   
    return resultBitmap; 
}

   
public static Bitmap UnsharpMean5x5( 
                                 this Bitmap sourceBitmap, 
                                 float factor = 1.0f) 
{ 
    Bitmap blurBitmap = ExtBitmap.ConvolutionFilter( 
                                  sourceBitmap,  
                                  Matrix.Mean5x5,  
                                  1.0 / 25.0); 

   
    Bitmap resultBitmap = 
           sourceBitmap.SubtractAddFactorImage( 
                        blurBitmap, factor); 

   
    return resultBitmap; 
}

Sample Images

The input/source image used in rendering the sample images shown in this article is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license and can be downloaded from Wikipedia:

The Original Image

Unsharp Gaussian 3×3

Unsharp Gaussian 5×5

Unsharp Mean 3×3

Unsharp Gaussian 5×5

C# How to: Difference Of Gaussians

Published May 18, 2013 Augmented Reality , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , New Version , Opensource 31 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blob detection, C#, Change detection, Code Sample, Computer vision, Convolution filters, Convolution Kernel, Convolution matrix, Difference of Gaussians, DoG, DoG Edge Detection, Edge Detect, Edge enhance, Feature extraction, Gaussian, Gaussian Blur, Graphic Filters, Image Noise, Image processing, Image Transform, Machine vision, Matrix, Pixel Filters, Pixel Manipulation, Step detection

Article purpose

In this article we explore the concept of Difference of Gaussians edge detection. This article implements image convolution as a means of achieving Gaussian blurring. All of the concepts explored are implemented by accessing and manipulating the raw pixel data exposed by an image, no GDI+ or conventional drawing code is required.

Sample source code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The concepts explored in this article can be easily replicated by making use of the Sample Application, which forms part of the associated sample source code accompanying this article.

When using the Difference Of Gaussians sample application you can specify a input/source image by clicking the Load Image button. The dropdown combobox towards the bottom middle part of the screen relates the various edge detection methods discussed.

If desired a user can save the resulting edge detection image to the local file system by clicking the Save Image button.

The following image is screenshot of the Difference Of Gaussians sample application in action:

What is Difference of Gaussians?

Difference of Gaussians, commonly abbreviated as DoG, is a method of implementing image edge detection. Central to the Difference of Gaussians method of edge detection is the application of Gaussian image blur.

From Wikipedia we gain the following explanation:

In imaging science, Difference of Gaussians is a feature enhancement algorithm that involves the subtraction of one blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing standard deviations. Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the difference of Gaussians is a band-pass filter that discards all but a handful of spatial frequencies that are present in the original grayscale image.

In simple terms Difference of Gaussians can be implemented by applying two Gaussian blurs of different intensity levels to the same source image. The resulting image is then created by subtracting the two images of different Gaussian blurring.

Applying a Convolution Matrix filter

In the sample source code accompanying this article Gaussian image blurring is applied by invoking the ConvolutionFilter method. This method accepts a two dimensional array of type double representing the convolution matrix/kernel. This method is also capable of first converting source images to grayscale, which can be specified as a method parameter. Resulting images sometimes tend to be very dark, which can be corrected by specifying a suitable bias value.

The following code snippet provides the implementation of the ConvolutionFilter method:

 private static Bitmap ConvolutionFilter(Bitmap sourceBitmap,  
                                     double[,] filterMatrix,  
                                          double factor = 1,  
                                               int bias = 0,  
                                     bool grayscale = false )  
{ 
     BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0, 
                              sourceBitmap.Width, sourceBitmap.Height), 
                                                ImageLockMode.ReadOnly,  
                                          PixelFormat.Format32bppArgb); 

  
     byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
     byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

  
     Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
     sourceBitmap.UnlockBits(sourceData); 

  
     if (grayscale == true) 
     {
         float rgb = 0; 

  
         for (int k = 0; k < pixelBuffer.Length; k += 4) 
         { 
             rgb = pixelBuffer[k] * 0.11f; 
             rgb += pixelBuffer[k + 1] * 0.59f; 
             rgb += pixelBuffer[k + 2] * 0.3f; 

  
             pixelBuffer[k] = (byte )rgb; 
             pixelBuffer[k + 1] = pixelBuffer[k]; 
             pixelBuffer[k + 2] = pixelBuffer[k]; 
             pixelBuffer[k + 3] = 255; 
         } 
     } 

  
     double blue = 0.0; 
     double green = 0.0; 
     double red = 0.0; 

  
     int filterWidth = filterMatrix.GetLength(1); 
     int filterHeight = filterMatrix.GetLength(0); 

  
     int filterOffset = (filterWidth-1) / 2; 
     int calcOffset = 0; 

  
     int byteOffset = 0; 

  
     for (int offsetY = filterOffset; offsetY <  
         sourceBitmap.Height - filterOffset; offsetY++) 
     { 
         for (int  offsetX = filterOffset; offsetX <  
             sourceBitmap.Width - filterOffset; offsetX++) 
         { 
             blue = 0; 
             green = 0; 
             red = 0; 

  
             byteOffset = offsetY *  
                          sourceData.Stride +  
                          offsetX * 4; 

   
             for (int  filterY = -filterOffset;  
                 filterY <= filterOffset; filterY++) 
             {
                 for (int  filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                 { 

   
                     calcOffset = byteOffset +  
                                  (filterX * 4) +  
                                  (filterY * sourceData.Stride); 

  
                     blue += (double)(pixelBuffer[calcOffset]) * 
                             filterMatrix[filterY + filterOffset,  
                                          filterX + filterOffset]; 

  
                     green += (double)(pixelBuffer[calcOffset + 1]) * 
                              filterMatrix[filterY + filterOffset,  
                                           filterX + filterOffset]; 

   
                     red += (double)(pixelBuffer[calcOffset + 2]) * 
                            filterMatrix[filterY + filterOffset,  
                                         filterX + filterOffset]; 
                 }
             }

   
             blue = factor * blue + bias; 
             green = factor * green + bias; 
             red = factor * red + bias; 

  
             if (blue > 255) 
             { blue = 255; } 
             else if (blue < 0) 
             { blue = 0; } 

  
             if (green > 255) 
             { green = 255; } 
             else if (green < 0) 
             { green = 0; } 

  
             if (red > 255) 
             { red = 255; } 
             else if (red < 0) 
             { red = 0; } 

  
             resultBuffer[byteOffset] = (byte )(blue); 
             resultBuffer[byteOffset + 1] = (byte )(green); 
             resultBuffer[byteOffset + 2] = (byte )(red); 
             resultBuffer[byteOffset + 3] = 255; 
        }
    } 

  
     Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
                                      sourceBitmap.Height); 
  
     BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                              resultBitmap.Width, resultBitmap.Height), 
                                               ImageLockMode .WriteOnly, 
                                          PixelFormat.Format32bppArgb); 

  
     Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
     resultBitmap.UnlockBits(resultData); 

   
     return resultBitmap; 
}

The Gaussian Matrix

The sample source code defines three Gaussian matrix/kernel values, a 3×3 matrix and two slightly different 5×5 matrices. The Gaussian3x3 matrix requires a factor of 1 / 16, the Gaussian5x5Type1 matrix a factor of 1 / 159 and the factor required by the Gaussian5x5Type2 equates to 1 / 256.

public static class Matrix
{
    public static double[,] Gaussian3x3
    {
        get
        {
            return new double[,]  
            { { 1, 2, 1, }, 
              { 2, 4, 2, },
              { 1, 2, 1, }, };
        }
    }

  
    public static double[,] Gaussian5x5Type1
    {
        get  
        {
            return new double[,]  
             { { 2, 04, 05, 04, 2  }, 
               { 4, 09, 12, 09, 4  }, 
               { 5, 12, 15, 12, 5  },
               { 4, 09, 12, 09, 4  },
               { 2, 04, 05, 04, 2  }, };
        }
    }

  
    public static double[,] Gaussian5x5Type2
    {
        get 
        {
            return new   double[,] 
             { {  1,   4,  6,  4,  1  }, 
               {  4,  16, 24, 16,  4  }, 
               {  6,  24, 36, 24,  6  },
               {  4,  16, 24, 16,  4  },
               {  1,   4,  6,  4,  1  }, };
        }
    }
}

Subtracting Images

When implementing the Difference of Gaussians method of edge detection after having applied two varying levels of Gaussian blurring the resulting images need to be subtracted. The sample source code associated with this article implements the SubtractImage extension method when subtracting images.

The following code snippet details the implementation of the SubtractImage extension method:

private static void SubtractImage(this Bitmap subtractFrom,  
                                  Bitmap subtractValue,  
                                  bool invert = false,
                                  int bias = 0) 
{ 
    BitmapData sourceData = 
               subtractFrom.LockBits(new Rectangle(0, 0, 
               subtractFrom.Width, subtractFrom.Height), 
               ImageLockMode.ReadWrite, 
               PixelFormat.Format32bppArgb); 

   
    byte[] resultBuffer = new byte[sourceData.Stride *
                                  sourceData.Height]; 

  
    Marshal.Copy(sourceData.Scan0, resultBuffer, 0,
                               resultBuffer.Length); 

   
    BitmapData subtractData =
               subtractValue.LockBits(new Rectangle(0, 0, 
               subtractValue.Width, subtractValue.Height), 
               ImageLockMode.ReadOnly, 
               PixelFormat.Format32bppArgb); 

   
    byte[] subtractBuffer = new byte[subtractData.Stride *  
                                     subtractData.Height]; 

   
    Marshal.Copy(subtractData.Scan0, subtractBuffer, 0,  
                                 subtractBuffer.Length); 

   
    subtractValue.UnlockBits(subtractData); 

   
    int blue = 0; 
    int green = 0; 
    int red = 0; 

   
    for (int k = 0; k < resultBuffer.Length &&  
                    k < subtractBuffer.Length; k += 4) 
    { 
        if (invert == true ) 
        { 
            blue = 255 - resultBuffer[k] -  
                   subtractBuffer[k] + bias; 

   
            green = 255 - resultBuffer[k + 1] -  
                    subtractBuffer[k + 1] + bias; 

   
            red = 255 - resultBuffer[k + 2] -  
                  subtractBuffer[k + 2] + bias; 
        } 
        else  
        { 
            blue = resultBuffer[k] -  
                   subtractBuffer[k] + bias; 

   
            green = resultBuffer[k + 1] -  
                    subtractBuffer[k + 1] + bias; 

   
            red = resultBuffer[k + 2] -  
                  subtractBuffer[k + 2] + bias; 
        } 

   
        blue = (blue < 0 ? 0 : (blue > 255 ? 255 : blue)); 
        green = (green < 0 ? 0 : (green > 255 ? 255 : green)); 
        red = (red < 0 ? 0 : (red > 255 ? 255 : red)); 

   
        resultBuffer[k] = (byte )blue; 
        resultBuffer[k + 1] = (byte )green; 
        resultBuffer[k + 2] = (byte )red; 
        resultBuffer[k + 3] = 255; 
    } 

   
    Marshal.Copy(resultBuffer, 0, sourceData.Scan0,  
                               resultBuffer.Length); 

   
    subtractFrom.UnlockBits(sourceData); 
}

Difference of Gaussians Extension methods

The sample source code implements Difference of Gaussians edge detection by means of two extension methods: DifferenceOfGaussians3x5Type1 and DifferenceOfGaussians3x5Type2. Both methods are virtually identical, the only difference being the 5×5 Gaussian matrix being implemented.

Both methods create two new images, each having a Gaussian blur of different levels of intensity applied. The two new images are subtracted in order to create a single resulting image.

The following source code snippet provides the implementation of the DifferenceOfGaussians3x5Type1 and DifferenceOfGaussians3x5Type2 extension methods:

public static Bitmap DifferenceOfGaussians3x5Type1(
                                  this Bitmap sourceBitmap,  
                                  bool grayscale = false, 
                                  bool invert = false, 
                                  int bias = 0) 
{
    Bitmap bitmap3x3 = ExtBitmap.ConvolutionFilter(sourceBitmap, 
                       Matrix.Gaussian3x3, 1.0 / 16.0, 
                       0, grayscale); 

  
    Bitmap bitmap5x5 = ExtBitmap.ConvolutionFilter(sourceBitmap, 
                       Matrix.Gaussian5x5Type1, 1.0 / 159.0,
                       0, grayscale); 

  
    bitmap3x3.SubtractImage(bitmap5x5, invert, bias); 

  
    return bitmap3x3; 
} 

  
public static Bitmap DifferenceOfGaussians3x5Type2(
                                  this Bitmap sourceBitmap,  
                                  bool grayscale = false, 
                                  bool invert = false, 
                                  int bias = 0) 
{ 
    Bitmap bitmap3x3 = ExtBitmap.ConvolutionFilter(sourceBitmap, 
                       Matrix.Gaussian3x3, 1.0 / 16.0, 
                       0, true ); 

  
    Bitmap bitmap5x5 = ExtBitmap.ConvolutionFilter(sourceBitmap, 
                       Matrix.Gaussian5x5Type2, 1.0 / 256.0,
                       0, true ); 

 
    bitmap3x3.SubtractImage(bitmap5x5, invert, bias); 

  
    return bitmap3x3; 
}

Sample Images

The original sample image used in this article is licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license. The original author is attributed as Andrew Dunn – http://www.andrewdunnphoto.com/

The Original Image

Difference Of Gaussians 3×5 Type1

Difference Of Gaussians 3×5 Type2

Difference Of Gaussians 3×5 Type1 Bias 128

Difference Of Gaussians 3×5 Type 2 Bias 96

C# How to: Image Edge Detection

Published May 11, 2013 Augmented Reality , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , Opensource , Wikipedia 32 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blob detection, C#, Change detection, Code Sample, Computer vision, Convolution filters, Convolution Kernel, Convolution matrix, Edge Detect, Edge enhance, Feature extraction, Gaussian, Gaussian Blur, Graphic Filters, Image Noise, Image processing, Image Transform, Kirsch, Laplacian, Laplacian matrix, Laplacian of Gaussian, Machine vision, Matrix, Pixel Filters, Pixel Manipulation, Prewitt, Sobel, Step detection

Article Purpose

The objective of this article is to explore various edge detection algorithms. The types of edge detection discussed are: Laplacian, Laplacian of Gaussian, Sobel, Prewitt and Kirsch. All instances are implemented by means of Image Convolution.

Sample source code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The concepts explored in this article can be easily replicated by making use of the Sample Application, which forms part of the associated sample source code accompanying this article.

When using the Image Edge Detection sample application you can specify a input/source image by clicking the Load Image button. The dropdown combobox towards the bottom middle part of the screen relates the various edge detection methods discussed.

If desired a user can save the resulting edge detection image to the local file system by clicking the Save Image button.

The following image is screenshot of the Image Edge Detection sample application in action:

Edge Detection

A good description of edge detection forms part of the main Edge Detection article on Wikipedia:

Edge detection is the name for a set of mathematical methods which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities. The points at which image brightness changes sharply are typically organized into a set of curved line segments termed edges. The same problem of finding discontinuities in 1D signals is known as step detection and the problem of finding signal discontinuities over time is known as change detection. Edge detection is a fundamental tool in image processing, machine vision and computer vision, particularly in the areas of feature detection and feature extraction.

Image Convolution

A good introduction article to Image Convolution can be found at: http://homepages.inf.ed.ac.uk/rbf/HIPR2/convolve.htm. From the article we learn the following:

Convolution is a simple mathematical operation which is fundamental to many common image processing operators. Convolution provides a way of `multiplying together’ two arrays of numbers, generally of different sizes, but of the same dimensionality, to produce a third array of numbers of the same dimensionality. This can be used in image processing to implement operators whose output pixel values are simple linear combinations of certain input pixel values.

In an image processing context, one of the input arrays is normally just a graylevel image. The second array is usually much smaller, and is also two-dimensional (although it may be just a single pixel thick), and is known as the kernel.

Single Matrix Convolution

The sample source code implements the ConvolutionFilter method, an extension method targeting the Bitmap class. The ConvolutionFilter method is intended to apply a user defined matrix and optionally covert an image to grayscale. The implementation as follows:

private static Bitmap ConvolutionFilter(Bitmap sourceBitmap, 
                                     double[,] filterMatrix, 
                                          double factor = 1, 
                                               int bias = 0, 
                                     bool grayscale = false) 
{
    BitmapData sourceData = 
                   sourceBitmap.LockBits(new Rectangle(0, 0,
                   sourceBitmap.Width, sourceBitmap.Height),
                                     ImageLockMode.ReadOnly, 
                                PixelFormat.Format32bppArgb);

  
    byte[] pixelBuffer = new byte[sourceData.Stride *
                                  sourceData.Height];

 
    byte[] resultBuffer = new byte[sourceData.Stride *
                                   sourceData.Height];

  
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,
                               pixelBuffer.Length);

 
    sourceBitmap.UnlockBits(sourceData);

  
    if(grayscale == true)
    {
        float rgb = 0;

  
        for(int k = 0; k < pixelBuffer.Length; k += 4)
        {
            rgb = pixelBuffer[k] * 0.11f;
            rgb += pixelBuffer[k + 1] * 0.59f;
            rgb += pixelBuffer[k + 2] * 0.3f;

  
            pixelBuffer[k] = (byte)rgb;
            pixelBuffer[k + 1] = pixelBuffer[k];
            pixelBuffer[k + 2] = pixelBuffer[k];
            pixelBuffer[k + 3] = 255;
        }
    }

  
    double blue = 0.0;
    double green = 0.0;
    double red = 0.0;

  
    int filterWidth = filterMatrix.GetLength(1);
    int filterHeight = filterMatrix.GetLength(0);

  
    int filterOffset = (filterWidth-1) / 2;
    int calcOffset = 0;

  
    int byteOffset = 0;

  
    for(int offsetY = filterOffset; offsetY < 
        sourceBitmap.Height - filterOffset; offsetY++)
    {
        for(int offsetX = filterOffset; offsetX < 
            sourceBitmap.Width - filterOffset; offsetX++)
        {
            blue = 0;
            green = 0;
            red = 0;

  
            byteOffset = offsetY * 
                         sourceData.Stride + 
                         offsetX * 4;

  
            for(int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++)
            {
                for(int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
               {

  
                   calcOffset = byteOffset + 
                                (filterX * 4) + 
                                (filterY * sourceData.Stride);

  
                   blue += (double)(pixelBuffer[calcOffset]) *
                           filterMatrix[filterY + filterOffset, 
                                        filterX + filterOffset];

  
                   green += (double)(pixelBuffer[calcOffset+1]) *
                            filterMatrix[filterY + filterOffset, 
                                         filterX + filterOffset];

  
                   red += (double)(pixelBuffer[calcOffset+2]) *
                          filterMatrix[filterY + filterOffset, 
                                       filterX + filterOffset];
                }
            }

  
            blue = factor * blue + bias;
            green = factor * green + bias;
            red = factor * red + bias;

  
            if(blue > 255)
            { blue = 255;}
            else if(blue < 0)
            { blue = 0;}

  
            if(green > 255)
            { green = 255;}
            else if(green < 0)
            { green = 0;}

  
            if(red > 255)
            { red = 255;}
            else if(red < 0)
            { red = 0;}

  
            resultBuffer[byteOffset] = (byte)(blue);
            resultBuffer[byteOffset + 1] = (byte)(green);
            resultBuffer[byteOffset + 2] = (byte)(red);
            resultBuffer[byteOffset + 3] = 255;
        }
    }

  
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, 
                                    sourceBitmap.Height);

  
    BitmapData resultData =
               resultBitmap.LockBits(new Rectangle(0, 0,
               resultBitmap.Width, resultBitmap.Height),
                                ImageLockMode.WriteOnly,
                            PixelFormat.Format32bppArgb);

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);
    resultBitmap.UnlockBits(resultData);

  
    return resultBitmap;
}

Horizontal and Vertical Matrix Convolution

The ConvolutionFilter extension method has been overloaded to accept two matrices, representing a vertical matrix and a horizontal matrix. The implementation as follows:

public static Bitmap ConvolutionFilter(this Bitmap sourceBitmap,
                                        double[,] xFilterMatrix,
                                        double[,] yFilterMatrix,
                                              double factor = 1,
                                                   int bias = 0,
                                         bool grayscale = false)
{
    BitmapData sourceData = 
                   sourceBitmap.LockBits(new Rectangle(0, 0,
                   sourceBitmap.Width, sourceBitmap.Height),
                                     ImageLockMode.ReadOnly,
                                PixelFormat.Format32bppArgb);

  
    byte[] pixelBuffer = new byte[sourceData.Stride * 
                                  sourceData.Height];

  
    byte[] resultBuffer = new byte[sourceData.Stride *
                                   sourceData.Height];

  
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,
                               pixelBuffer.Length);

  
    sourceBitmap.UnlockBits(sourceData);

  
    if (grayscale == true)
    {
        float rgb = 0;

  
        for (int k = 0; k < pixelBuffer.Length; k += 4)
        {
            rgb = pixelBuffer[k] * 0.11f;
            rgb += pixelBuffer[k + 1] * 0.59f;
            rgb += pixelBuffer[k + 2] * 0.3f;

  
            pixelBuffer[k] = (byte)rgb;
            pixelBuffer[k + 1] = pixelBuffer[k];
            pixelBuffer[k + 2] = pixelBuffer[k];
            pixelBuffer[k + 3] = 255;
        }
    }

  
    double blueX = 0.0;
    double greenX = 0.0;
    double redX = 0.0;

  
    double blueY = 0.0;
    double greenY = 0.0;
    double redY = 0.0;

  
    double blueTotal = 0.0;
    double greenTotal = 0.0;
    double redTotal = 0.0;

  
    int filterOffset = 1;
    int calcOffset = 0;

  
    int byteOffset = 0;

  
    for (int offsetY = filterOffset; offsetY <
        sourceBitmap.Height - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            sourceBitmap.Width - filterOffset; offsetX++)
        {
            blueX = greenX = redX = 0;
            blueY = greenY = redY = 0;

  
            blueTotal = greenTotal = redTotal = 0.0;

  
            byteOffset = offsetY *
                         sourceData.Stride +
                         offsetX * 4;

  
            for (int filterY = -filterOffset;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
                {
                    calcOffset = byteOffset +
                                 (filterX * 4) +
                                 (filterY * sourceData.Stride);

  
                    blueX += (double)
                              (pixelBuffer[calcOffset]) *
                              xFilterMatrix[filterY + 
                                            filterOffset,
                                            filterX + 
                                            filterOffset];

  
                    greenX += (double)
                          (pixelBuffer[calcOffset + 1]) *
                              xFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    redX += (double)
                          (pixelBuffer[calcOffset + 2]) *
                              xFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    blueY += (double)
                              (pixelBuffer[calcOffset]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    greenY += (double)
                          (pixelBuffer[calcOffset + 1]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    redY += (double)
                          (pixelBuffer[calcOffset + 2]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];
                }
            }

  
            blueTotal = Math.Sqrt((blueX * blueX) +
                                  (blueY * blueY));

  
            greenTotal = Math.Sqrt((greenX * greenX) +
                                   (greenY * greenY));

  
            redTotal = Math.Sqrt((redX * redX) +
                                 (redY * redY));

  
            if (blueTotal > 255)
            { blueTotal = 255; }
            else if (blueTotal < 0)
            { blueTotal = 0; }

  
            if (greenTotal > 255)
            { greenTotal = 255; }
            else if (greenTotal < 0)
            { greenTotal = 0; }

  
            if (redTotal > 255)
            { redTotal = 255; }
            else if (redTotal < 0)
            { redTotal = 0; }

  
            resultBuffer[byteOffset] = (byte)(blueTotal);
            resultBuffer[byteOffset + 1] = (byte)(greenTotal);
            resultBuffer[byteOffset + 2] = (byte)(redTotal);
            resultBuffer[byteOffset + 3] = 255;
        }
    }

  
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
                                     sourceBitmap.Height);

  
    BitmapData resultData =
               resultBitmap.LockBits(new Rectangle(0, 0,
               resultBitmap.Width, resultBitmap.Height),
                                ImageLockMode.WriteOnly,
                            PixelFormat.Format32bppArgb);

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);
    resultBitmap.UnlockBits(resultData);

  
    return resultBitmap;
}

Original Sample Image

The original source image used to create all of the edge detection sample images in this article has been licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license. The original image is attributed to Kenneth Dwain Harrelson and can be downloaded from Wikipedia.

Laplacian Edge Detection

The Laplacian method of edge detection counts as one of the commonly used edge detection implementations. From Wikipedia we gain the following definition:

Discrete Laplace operator is often used in image processing e.g. in edge detection and motion estimation applications. The discrete Laplacian is defined as the sum of the second derivatives Laplace operator Coordinate expressions and calculated as sum of differences over the nearest neighbours of the central pixel.

A number of matrix/kernel variations may be applied with results ranging from slight to fairly pronounced. In the following sections of this article we explore two common matrix implementations, 3×3 and 5×5.

Laplacian 3×3

When implementing a 3×3 Laplacian matrix you will notice little difference between colour and grayscale result images.

public static Bitmap 
Laplacian3x3Filter(this Bitmap sourceBitmap, 
                      bool grayscale = true)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                Matrix.Laplacian3x3,
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}

public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
}

Laplacian 3×3

Laplacian 3×3 Grayscale

Laplacian 5×5

The 5×5 Laplacian matrix produces result images with a noticeable difference between colour and grayscale images. The detected edges are expressed in a fair amount of fine detail, although the Laplacian matrix has a tendency to be sensitive to image noise.

public static Bitmap 
Laplacian5x5Filter(this Bitmap sourceBitmap, 
                      bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                Matrix.Laplacian5x5,
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}

public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}

Laplacian 5×5

Laplacian 5×5 Grayscale

Laplacian of Gaussian

The Laplacian of Gaussian (LoG) is a common variation of the Laplacian filter. Laplacian of Gaussian is intended to counter the noise sensitivity of the regular Laplacian filter.

Laplacian of Gaussian attempts to remove image noise by implementing image smoothing by means of a Gaussian blur. In order to optimize performance we can calculate a single matrix representing a Gaussian blur and Laplacian matrix.

public static Bitmap 
LaplacianOfGaussian(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                         Matrix.LaplacianOfGaussian, 
                                       1.0, 0, true);

 
    return resultBitmap;
}

public static double[,] LaplacianOfGaussian
{ 
    get   
    { 
        return new double[,]
        { {  0,  0, -1,  0,  0 },  
          {  0, -1, -2, -1,  0 },  
          { -1, -2, 16, -2, -1 }, 
          {  0, -1, -2, -1,  0 }, 
          {  0,  0, -1,  0,  0 } };
    } 
}

Laplacian of Gaussian

Laplacian (3×3) of Gaussian (3×3)

Different matrix variations can be combined in an attempt to produce results best suited to the input image. In this case we first apply a 3×3 Gaussian blur followed by a 3×3 Laplacian filter.

public static Bitmap 
Laplacian3x3OfGaussian3x3Filter(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                 Matrix.Gaussian3x3,
                                1.0 / 16.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
}

public static double[,] Gaussian3x3
{ 
   get   
   { 
       return new double[,]
       { { 1, 2, 1, },  
         { 2, 4, 2, },  
         { 1, 2, 1, } }; 
   } 
}

Laplacian 3×3 Of Gaussian 3×3

Laplacian (3×3) of Gaussian (5×5 – Type 1)

In this scenario we apply a variation of a 5×5 Gaussian blur followed by a 3×3 Laplacian filter.

public static Bitmap 
Laplacian3x3OfGaussian5x5Filter1(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type1,
                               1.0 / 159.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
}

public static double[,] Gaussian5x5Type1 
{ 
   get   
   { 
       return new double[,]   
       { { 2, 04, 05, 04, 2 },  
         { 4, 09, 12, 09, 4 },  
         { 5, 12, 15, 12, 5 }, 
         { 4, 09, 12, 09, 4 }, 
         { 2, 04, 05, 04, 2 }, }; 
   } 
}

Laplacian 3×3 Of Gaussian 5×5 – Type 1

Laplacian (3×3) of Gaussian (5×5 – Type 2)

The following implementation is very similar to the previous implementation. Applying a variation of a 5×5 Gaussian blur results in slight differences.

public static Bitmap 
Laplacian3x3OfGaussian5x5Filter2(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type2,
                               1.0 / 256.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
}

public static double[,] Gaussian5x5Type2 
{ 
   get   
   {
       return new double[,]  
       { {  1,   4,  6,  4,  1 },  
         {  4,  16, 24, 16,  4 },  
         {  6,  24, 36, 24,  6 }, 
         {  4,  16, 24, 16,  4 }, 
         {  1,   4,  6,  4,  1 }, }; 
   }
}

Laplacian 3×3 Of Gaussian 5×5 – Type 2

Laplacian (5×5) of Gaussian (3×3)

This variation of the Laplacian of Gaussian filter implements a 3×3 Gaussian blur, followed by a 5×5 Laplacian matrix. The resulting image appears significantly brighter when compared to a 3×3 Laplacian matrix.

public static Bitmap 
Laplacian5x5OfGaussian3x3Filter(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                 Matrix.Gaussian3x3,
                                1.0 / 16.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap,
                         Matrix.Laplacian5x5, 1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}

public static double[,] Gaussian3x3
{ 
   get   
   { 
       return new double[,]
       { { 1, 2, 1, },  
         { 2, 4, 2, },  
         { 1, 2, 1, } }; 
   } 
}

Laplacian 5×5 Of Gaussian 3×3

Laplacian (5×5) of Gaussian (5×5 – Type 1)

Implementing a larger Gaussian blur matrix results in a higher degree of image smoothing, equating to less image noise.

public static Bitmap 
Laplacian5x5OfGaussian5x5Filter1(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type1,
                               1.0 / 159.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap,
                         Matrix.Laplacian5x5, 1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}

public static double[,] Gaussian5x5Type1 
{ 
   get   
   { 
       return new double[,]   
       { { 2, 04, 05, 04, 2 },  
         { 4, 09, 12, 09, 4 },  
         { 5, 12, 15, 12, 5 }, 
         { 4, 09, 12, 09, 4 }, 
         { 2, 04, 05, 04, 2 }, }; 
   } 
}

Laplacian 5×5 Of Gaussian 5×5 – Type 1

Laplacian (5×5) of Gaussian (5×5 – Type 2)

The variation of Gaussian blur most applicable when implementing a Laplacian of Gaussian filter depends on image noise expressed by a source image. In this scenario the first variations (Type 1) appears to result in less image noise.

public static Bitmap 
Laplacian5x5OfGaussian5x5Filter2(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type2, 
                               1.0 / 256.0, 0, true);

 
    resultBitmap = 
           ExtBitmap.ConvolutionFilter(resultBitmap, 
                                Matrix.Laplacian5x5, 
                                      1.0, 0, false);

 
    return resultBitmap;
}

public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}

public static double[,] Gaussian5x5Type2 
{ 
   get   
   {
       return new double[,]  
       { {  1,   4,  6,  4,  1 },  
         {  4,  16, 24, 16,  4 },  
         {  6,  24, 36, 24,  6 }, 
         {  4,  16, 24, 16,  4 }, 
         {  1,   4,  6,  4,  1 }, }; 
   }
}

Laplacian 5×5 Of Gaussian 5×5 – Type 2

Sobel Edge Detection

Sobel edge detection is another common implementation of edge detection. We gain the following quote from Wikipedia:

The Sobel operator is used in image processing, particularly within edge detection algorithms. Technically, it is a discrete differentiation operator, computing an approximation of the gradient of the image intensity function. At each point in the image, the result of the Sobel operator is either the corresponding gradient vector or the norm of this vector. The Sobel operator is based on convolving the image with a small, separable, and integer valued filter in horizontal and vertical direction and is therefore relatively inexpensive in terms of computations. On the other hand, the gradient approximation that it produces is relatively crude, in particular for high frequency variations in the image.

Unlike the Laplacian filters discussed earlier, Sobel filter results differ significantly when comparing colour and grayscale images. The Sobel filter tends to be less sensitive to image noise compared to the Laplacian filter. The detected edge lines are not as finely detailed/granular as the detected edge lines resulting from Laplacian filters.

public static Bitmap 
Sobel3x3Filter(this Bitmap sourceBitmap, 
                  bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                          Matrix.Sobel3x3Horizontal, 
                            Matrix.Sobel3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}

 
public static double[,] Sobel3x3Horizontal
{ 
   get   
   {
       return new double[,]  
       { { -1,  0,  1, },  
         { -2,  0,  2, },  
         { -1,  0,  1, }, }; 
   } 
}

public static double[,] Sobel3x3Vertical 
{ 
   get   
   { 
       return new double[,]  
       { {  1,  2,  1, },  
         {  0,  0,  0, },  
         { -1, -2, -1, }, }; 
   } 
}

Sobel 3×3

Sobel 3×3 Grayscale

Prewitt Edge Detection

As with the other methods of edge detection discussed in this article the Prewitt edge detection method is also a fairly common implementation. From Wikipedia we gain the following quote:

The Prewitt operator is used in image processing, particularly within edge detection algorithms. Technically, it is a discrete differentiation operator, computing an approximation of the gradient of the image intensity function. At each point in the image, the result of the Prewitt operator is either the corresponding gradient vector or the norm of this vector. The Prewitt operator is based on convolving the image with a small, separable, and integer valued filter in horizontal and vertical direction and is therefore relatively inexpensive in terms of computations. On the other hand, the gradient approximation which it produces is relatively crude, in particular for high frequency variations in the image. The Prewitt operator was developed by Judith M. S. Prewitt.

In simple terms, the operator calculates the gradient of the image intensity at each point, giving the direction of the largest possible increase from light to dark and the rate of change in that direction. The result therefore shows how "abruptly" or "smoothly" the image changes at that point, and therefore how likely it is that that part of the image represents an edge, as well as how that edge is likely to be oriented. In practice, the magnitude (likelihood of an edge) calculation is more reliable and easier to interpret than the direction calculation.

Similar to the Sobel filter, resulting images express a significant difference when comparing colour and grayscale images.

public static Bitmap 
PrewittFilter(this Bitmap sourceBitmap, 
                 bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                        Matrix.Prewitt3x3Horizontal, 
                          Matrix.Prewitt3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}

public static double[,] Prewitt3x3Horizontal 
{ 
   get   
   { 
       return new double[,]  
       { { -1,  0,  1, },  
         { -1,  0,  1, },  
         { -1,  0,  1, }, }; 
   } 
}

  
public static double[,] Prewitt3x3Vertical 
{ 
   get   
   { 
       return new double[,]  
       { {  1,  1,  1, },  
         {  0,  0,  0, },  
         { -1, -1, -1, }, }; 
   }
}

Prewitt

Prewitt Grayscale

Kirsch Edge Detection

The Kirsch edge detection method is often implemented in the form of Compass edge detection. In the following scenario we only implement two components: Horizontal and Vertical. Resulting images tend to have a high level of brightness.

public static Bitmap 
KirschFilter(this Bitmap sourceBitmap, 
                bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                         Matrix.Kirsch3x3Horizontal, 
                           Matrix.Kirsch3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}

public static double[,] Kirsch3x3Horizontal 
{ 
   get   
   {
       return new double[,]  
       { {  5,  5,  5, },  
         { -3,  0, -3, },  
         { -3, -3, -3, }, }; 
   } 
}

public static double[,] Kirsch3x3Vertical
{ 
   get   
   { 
       return new double[,]  
       { {  5, -3, -3, },  
         {  5,  0, -3, },  
         {  5, -3, -3, }, }; 
   } 
}

Kirsch

Kirsch Grayscale

Posts Tagged 'Edge enhance'

Article Purpose

Sample Source Code

Using the Sample Application

Fuzzy Blur Overview

Mean Filter Blurring

Boolean Edge Detection without a local threshold

Implementing a Mean Filter

Implementing Boolean Edge Detection

Implementing a Fuzzy Blur Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Morphological Boundary Extraction

Boundary Sharpening

Boundary Tracing

Implementing Morphological Erosion and Dilation

Implementing Image Addition

Implementing Image Subtraction

Implementing Image Boundary Extraction

Implementing Image Boundary Sharpening

Implementing Image Boundary Tracing

Implementing a Wrapper Method

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article purpose

Sample Source code

Using the Sample Application

What is Image Unsharp Masking?

Applying a Convolution Matrix filter

Subtracting and Adding Images

Matrix Definition

Implementing Image Unsharpening

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article purpose

Sample source code

Using the Sample Application

What is Difference of Gaussians?

Applying a Convolution Matrix filter

The Gaussian Matrix

Subtracting Images

Difference of Gaussians Extension methods

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample source code

Using the Sample Application

Edge Detection

Image Convolution

Single Matrix Convolution

Horizontal and Vertical Matrix Convolution

Original Sample Image

Laplacian Edge Detection

Laplacian 3×3

Laplacian 5×5

Laplacian of Gaussian

Laplacian (3×3) of Gaussian (3×3)

Laplacian (3×3) of Gaussian (5×5 – Type 1)

Laplacian (3×3) of Gaussian (5×5 – Type 2)

Laplacian (5×5) of Gaussian (3×3)

Laplacian (5×5) of Gaussian (5×5 – Type 1)

Laplacian (5×5) of Gaussian (5×5 – Type 2)

Sobel Edge Detection

Prewitt Edge Detection

Kirsch Edge Detection

Related Articles and Feedback

Rate this:

Share this:

Dewald Esterhuizen