Article Purpose
This article is intended to serve as an introduction to the concepts related to creating and processing convolution filters being applied on images. The Convolution filters discussed are: Blur, Gaussian Blur, Soften, Motion Blur, High Pass, Edge Detect, Sharpen and Emboss.
Sample Source code
This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application
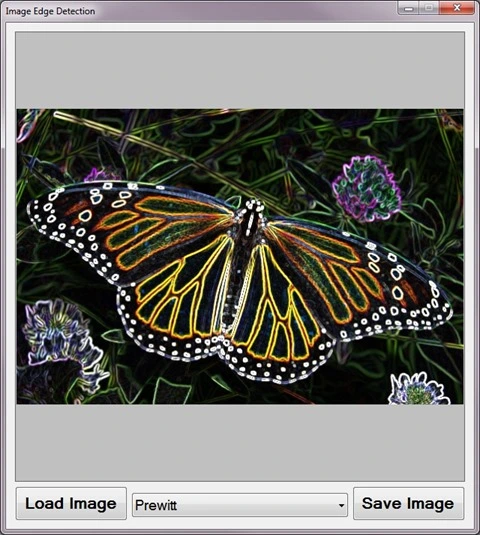
A Sample Application has been included with this article’s sample source code. The Sample Application has been developed to target the Windows Forms platform. Using the Sample Application users are able to select a source/input image from the local file system and from a drop down ComboBox select a Convolution filter to apply. Filtered images can be saved to the local file system when a user clicks the ‘Save’ button.
The following screenshot shows the Image Convolution Filter sample application in action.

Image Convolution
Before delving into discussions on technical implementation details it is important to have a good understanding of the concepts behind Image Convolution.
In relation to image processing Convolution can be considered as algorithms being implemented resulting in translating input/source images. Algorithms being applied generally take the form of accepting two input values and producing a third value considered to be a modified version of one of the input values.
Image Convolution can be implemented to produce image filters such as: Blurring, Smoothing, Edge Detection, Sharpening and Embossing. The resulting filtered images still bares a relation to the input source image.
Convolution Matrix
In this article we will be implementing Convolution through means of a matrix or kernel representing the algorithms required to produce resulting filtered images. A Matrix should be considered as a two dimensional array or grid. It is required that the number or rows and columns be of an equal size, which is furthermore required to not be a factor of two. Examples of valid matrix dimensions could be 3×3 or 5×5. Dimensions such as 2×2 or 4×4 would not be valid. Generally the sum total of all the values expressed in a matrix equates to one, although it is not a strict requirement.
The following table represents an example matrix/kernel:
An important aspect to keep in mind: When implementing a convolution matrix the value of a pixel will be determined by the values of the pixel’s neighbouring pixels. The values contained in a matrix represent factor values intended to be multiplied with pixel values. In a convolution matrix the centre pixel represents the pixel currently being modified. Neighbouring matrix values express the factor to be applied to the corresponding neighbouring pixels in regards to the pixel currently being modified.
The ConvolutionFilterBase class
The sample code defines the abstract class ConvolutionFilterBase. This class is intended to represent the minimum requirements of a convolution matrix. When defining a convolution matrix we will be inheriting from the ConvolutionFilterBase class. Because this class and its members have been defined as abstract, implementing classes are required to implement all defined abstract members.
The following code snippet details the ConvolutionFilterBase definition:
public abstract class ConvolutionFilterBase
{
public abstract string FilterName
{
get;
}
public abstract double Factor
{
get;
}
public abstract double Bias
{
get;
}
public abstract double[,] FilterMatrix
{
get;
}
}
As to be expected the member property FilterMatrix is intended to represent a two dimensional array containing a convolution matrix. In some instances when the sum total of matrix values do not equate to 1 a filter might implement a Factor value other than the default of 1. Additionally some filters may also require a Bias value to be added the final result value when calculating the matrix.
Calculating a Convolution Filter
Calculating convolution filters and creating the resulting Bitmap images can be achieved by invoking the ConvolutionFilter method. This method is defined as an extension method targeting the Bitmap class. The definition of the ConvolutionFilter extension method as follows:
public static Bitmap ConvolutionFilter<T>(this Bitmap sourceBitmap, T filter)
where T : ConvolutionFilterBase
{
BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0,
sourceBitmap.Width, sourceBitmap.Height),
ImageLockMode.ReadOnly, PixelFormat.Format32bppArgb);
byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height];
byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height];
Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length);
sourceBitmap.UnlockBits(sourceData);
double blue = 0.0;
double green = 0.0;
double red = 0.0;
int filterWidth = filter.FilterMatrix.GetLength(1);
int filterHeight = filter.FilterMatrix.GetLength(0);
int filterOffset = (filterWidth-1) / 2;
int calcOffset = 0;
int byteOffset = 0;
for (int offsetY = filterOffset; offsetY <
sourceBitmap.Height - filterOffset; offsetY++)
{
for (int offsetX = filterOffset; offsetX <
sourceBitmap.Width - filterOffset; offsetX++)
{
blue = 0;
green = 0;
red = 0;
byteOffset = offsetY *
sourceData.Stride +
offsetX * 4;
for (int filterY = -filterOffset;
filterY <= filterOffset; filterY++)
{
for (int filterX = -filterOffset;
filterX <= filterOffset; filterX++)
{
calcOffset = byteOffset +
(filterX * 4) +
(filterY * sourceData.Stride);
blue += (double)(pixelBuffer[calcOffset]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
green += (double)(pixelBuffer[calcOffset + 1]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
red += (double)(pixelBuffer[calcOffset + 2]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
}
}
blue = filter.Factor * blue + filter.Bias;
green = filter.Factor * green + filter.Bias;
red = filter.Factor * red + filter.Bias;
if (blue > 255)
{ blue = 255; }
else if (blue < 0)
{ blue = 0; }
if (green > 255)
{ green = 255; }
else if (green < 0)
{ green = 0; }
if (red > 255)
{ red = 255; }
else if (red < 0)
{ red = 0; }
resultBuffer[byteOffset] = (byte)(blue);
resultBuffer[byteOffset + 1] = (byte)(green);
resultBuffer[byteOffset + 2] = (byte)(red);
resultBuffer[byteOffset + 3] = 255;
}
}
Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height);
BitmapData resultData = resultBitmap.LockBits(new Rectangle(0, 0,
resultBitmap.Width, resultBitmap.Height),
ImageLockMode.WriteOnly, PixelFormat.Format32bppArgb);
Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length);
resultBitmap.UnlockBits(resultData);
return resultBitmap;
}
The following section provides a detailed discussion of the ConvolutionFilter extension method.
ConvolutionFilter<T> – Method Signature
public static Bitmap ConvolutionFilter<T>
(this Bitmap sourceBitmap,
T filter)
where T : ConvolutionFilterBase
The ConvolutionFilter method defines a generic type T constrained by the requirement to be of type ConvolutionFilterBase. The filter parameter being of generic type T has to be of type ConvolutionFilterBase or a type which inherits from the ConvolutionFilterBase class.
Notice how the sourceBitmap parameter type definition is preceded by the this keyword indicating the method can be implemented as an extension method. Keep in mind extension methods are required to be declared as static.
The sourceBitmap parameter represents the source/input Bitmap upon which the filter is to be applied. Note that the ConvolutionFilter method is implemented as immutable. The input parameter values are not modified, instead a new Bitmap instance will be created and returned.
ConvolutionFilter<T> – Creating the Data Buffer
BitmapData sourceData = sourceBitmap.LockBits
(new Rectangle(0, 0,
sourceBitmap.Width,
sourceBitmap.Height),
ImageLockMode.ReadOnly,
PixelFormat.Format32bppArgb);
byte[] pixelBuffer = new byte[sourceData.Stride *
sourceData.Height];
byte[] resultBuffer = new byte[sourceData.Stride *
sourceData.Height];
Marshal.Copy(sourceData.Scan0, pixelBuffer,
0, pixelBuffer.Length);
sourceBitmap.UnlockBits(sourceData);
In order to access the underlying ARGB values from a Bitmap object we first need to lock the Bitmap into memory by invoking the Bitmap.LockBits method. Locking a Bitmap into memory prevents the Garbage Collector from moving a Bitmap object to a new location in memory.
When invoking the Bitmap.LockBits method the source code instantiates a BitmapData object from the return value. The BitmapData.Stride property represents the number of bytes in a single Bitmap pixel row. In this scenario the BitmapData.Stride property should be equal to the Bitmap’s width in pixels multiplied by four seeing as every pixel consists of four bytes: Alpha, Red, Green and Blue.
The ConvolutionFilter method defines two byte buffers, of which the size is set to equal the size of the Bitmap’s underlying data. The BitmapData property BitmapData.Scan0 of type IntPtr represents the memory address of the first byte value of a Bitmap’s underlying byte buffer. Using the Marshal.Copy method we specify the starting point memory address from where to start copying the Bitmap’s byte buffer.
Important to remember is the next operation being performed: invoking the Bitmap.UnlockBits method. If a Bitmap has been locked into memory ensure releasing the lock by invoking the Bitmap.UnlockBits method.
ConvolutionFilter<T> – Iterating Rows and Columns
double blue = 0.0;
double green = 0.0;
double red = 0.0;
int filterWidth = filter.FilterMatrix.GetLength(1);
int filterHeight = filter.FilterMatrix.GetLength(0);
int filterOffset = (filterWidth-1) / 2;
int calcOffset = 0;
int byteOffset = 0;
for (int offsetY = filterOffset; offsetY <
sourceBitmap.Height - filterOffset; offsetY++)
{
for (int offsetX = filterOffset; offsetX <
sourceBitmap.Width - filterOffset; offsetX++)
{
blue = 0;
green = 0;
red = 0;
byteOffset = offsetY *
sourceData.Stride +
offsetX * 4;
The ConvolutionFilter method employs two for loops in order to iterate each pixel represented in the ARGB data buffer. Defining two for loops to iterate a one dimensional array simplifies the concept of accessing the array in terms of rows and columns.
Note that the inner loop is limited to the width of the source/input Bitmap parameter, in other words the number of horizontal pixels. Remember that the data buffer represents four bytes, Alpha, Red, Green and Blue, for each pixel. The inner loop therefore iterates entire pixels.
As discussed earlier the filter matrix has to be declared as a two dimensional array with the same odd number of rows and columns. If the current pixel being processed relates to the element at the centre of the matrix, the width of the matrix less one divided by two equates to the neighbouring pixel index values.
The index of the current pixel can be calculated by multiplying the current row index (offsetY) and the number of ARGB byte values per row of pixels (sourceData.Stride), to which is added the current column/pixel index (offsetX) multiplied by four.
ConvolutionFilter<T> – Iterating the Matrix
for (int filterY = -filterOffset;
filterY <= filterOffset; filterY++)
{
for (int filterX = -filterOffset;
filterX <= filterOffset; filterX++)
{
calcOffset = byteOffset +
(filterX * 4) +
(filterY * sourceData.Stride);
blue += (double)(pixelBuffer[calcOffset]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
green += (double)(pixelBuffer[calcOffset + 1]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
red += (double)(pixelBuffer[calcOffset + 2]) *
filter.FilterMatrix[filterY + filterOffset,
filterX + filterOffset];
}
}
The ConvolutionFilter method iterates the two dimensional matrix by implementing two for loops, iterating rows and for each row iterating columns. Both loops have been declared to have a starting point equal to the negative value of half the matrix length (filterOffset). Initiating the loops with negative values simplifies implementing the concept of neighbouring pixels.
The first statement performed within the inner loop calculates the index of the neighbouring pixel in relation to the current pixel. Next the matrix value is applied as a factor to the corresponding neighbouring pixel’s individual colour components. The results are added to the totals variables blue, green and red.
In regards to each iteration iterating in terms of an entire pixel, to access individual colour components the source code adds the required colour component offset. Note: ARGB colour components are in fact expressed in reversed order: Blue, Green, Red and Alpha. In other words, a pixel’s first byte (offset 0) represents Blue, the second (offset 1) represents Green, the third (offset 2) represents Red and the last (offset 3) representing the Alpha component.
ConvolutionFilter<T> – Applying the Factor and Bias
blue = filter.Factor * blue + filter.Bias;
green = filter.Factor * green + filter.Bias;
red = filter.Factor * red + filter.Bias;
if (blue > 255)
{ blue = 255; }
else if (blue < 0)
{ blue = 0; }
if (green > 255)
{ green = 255; }
else if (green < 0)
{ green = 0; }
if (red > 255)
{ red = 255; }
else if (red < 0)
{ red = 0; }
resultBuffer[byteOffset] = (byte)(blue);
resultBuffer[byteOffset + 1] = (byte)(green);
resultBuffer[byteOffset + 2] = (byte)(red);
resultBuffer[byteOffset + 3] = 255;
After iterating the matrix and calculating the matrix values of the current pixel’s Red, Green and Blue colour components we apply the Factor and add the Bias defined by the filter parameter.
Colour components may only contain a value ranging from 0 to 255 inclusive. Before we assign the newly calculated colour component value we ensure that the value falls within the required range. Values which exceed 255 are set to 255 and values less than 0 are set to 0. Note that assignment is implemented in terms of the result buffer, the original source image buffer remains unchanged.
ConvolutionFilter<T> – Returning the Result
Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
sourceBitmap.Height);
BitmapData resultData = resultBitmap.LockBits(
new Rectangle(0, 0,
resultBitmap.Width,
resultBitmap.Height),
ImageLockMode.WriteOnly,
PixelFormat.Format32bppArgb);
Marshal.Copy(resultBuffer, 0, resultData.Scan0,
resultBuffer.Length);
resultBitmap.UnlockBits(resultData);
return resultBitmap;
The final steps performed by the ConvolutionFilter method involves creating a new Bitmap object instance and copying the calculated result buffer. In a similar fashion to reading underlying pixel data we copy the result buffer to the Bitmap object.
Creating Filters
The main requirement when creating a filter is to inherit from the abstract ConvolutionBaseFilter class. The following sections of this article will discuss various filter types and variations where applicable.
To illustrate the different effects resulting from applying filters all of the filters discussed make use of the same source image. The original image file is licensed under the Creative Commons Attribution 2.0 Generic license and can be downloaded from:
http://commons.wikimedia.org/wiki/File:Ara_macao_-on_a_small_bicycle-8.jpg

Blur Filters
Image blurring is typically used to reduce image noise and detail. The filter’s matrix size affects the level of blurring. A larger matrix results in higher level of blurring, whereas a smaller matrix results in a lesser level of blurring.
Blur3x3Filter
The Blur3x3Filter results in a slight to medium level of image blurring. The matrix consists of 9 elements in a 3×3 configuration.

public class Blur3x3Filter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Blur3x3Filter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0.0, 0.2, 0.0, },
{ 0.2, 0.2, 0.2, },
{ 0.0, 0.2, 0.2, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Blur5x5Filter
The Blur5x5Filter results in a medium level of image blurring. The matrix consists of 25 elements in a 5×5 configuration. Notice the factor of 1.0 / 13.0.

public class Blur5x5Filter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Blur5x5Filter"; }
}
private double factor = 1.0 / 13.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, 0, 1, 0, 0, },
{ 0, 1, 1, 1, 0, },
{ 1, 1, 1, 1, 1, },
{ 0, 1, 1, 1, 0, },
{ 0, 0, 1, 0, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Gaussian3x3BlurFilter
The Gaussian3x3BlurFilter implements a Gaussian blur through a matrix of 9 elements in a 3×3 configuration. The sum total of all matrix elements equal 16, therefore the Factor is defined as 1.0 / 16.0. Applying this filter results in a slight to medium level of blurring.

public class Gaussian3x3BlurFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Gaussian3x3BlurFilter"; }
}
private double factor = 1.0 / 16.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 1, 2, 1, },
{ 2, 4, 2, },
{ 1, 2, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Gaussian5x5BlurFilter
The Gaussian5x5BlurFilter implements a Gaussian blur through a matrix of 25 elements in a 5×5 configuration. The sum total of all matrix elements equal 159, therefore the Factor is defined as 1.0 / 159.0. Applying this filter results in a medium level of blurring.

public class Gaussian5x5BlurFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Gaussian5x5BlurFilter"; }
}
private double factor = 1.0 / 159.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 2, 04, 05, 04, 2, },
{ 4, 09, 12, 09, 4, },
{ 5, 12, 15, 12, 5, },
{ 4, 09, 12, 09, 4, },
{ 2, 04, 05, 04, 2, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
MotionBlurFilter
By implementing the MotionBlurFilter resulting images indicate the appearance of a high level of blurring associated with motion/movement. This filter is a combination of left to right and right to left motion blurring. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "MotionBlurFilter"; }
}
private double factor = 1.0 / 18.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 1, 0, 0, 0, 0, 0, 0, 0, 1, },
{ 0, 1, 0, 0, 0, 0, 0, 1, 0, },
{ 0, 0, 1, 0, 0, 0, 1, 0, 0, },
{ 0, 0, 0, 1, 0, 1, 0, 0, 0, },
{ 0, 0, 0, 0, 1, 0, 0, 0, 0, },
{ 0, 0, 0, 1, 0, 1, 0, 0, 0, },
{ 0, 0, 1, 0, 0, 0, 1, 0, 0, },
{ 0, 1, 0, 0, 0, 0, 0, 1, 0, },
{ 1, 0, 0, 0, 0, 0, 0, 0, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
MotionBlurLeftToRightFilter
The MotionBlurLeftToRightFilter creates the effect of blurring as a result of left to right movement. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurLeftToRightFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "MotionBlurLeftToRightFilter"; }
}
private double factor = 1.0 / 9.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 1, 0, 0, 0, 0, 0, 0, 0, 0, },
{ 0, 1, 0, 0, 0, 0, 0, 0, 0, },
{ 0, 0, 1, 0, 0, 0, 0, 0, 0, },
{ 0, 0, 0, 1, 0, 0, 0, 0, 0, },
{ 0, 0, 0, 0, 1, 0, 0, 0, 0, },
{ 0, 0, 0, 0, 0, 1, 0, 0, 0, },
{ 0, 0, 0, 0, 0, 0, 1, 0, 0, },
{ 0, 0, 0, 0, 0, 0, 0, 1, 0, },
{ 0, 0, 0, 0, 0, 0, 0, 0, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
MotionBlurRightToLeftFilter
The MotionBlurRightToLeftFilter creates the effect of blurring as a result of right to left movement. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurRightToLeftFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "MotionBlurRightToLeftFilter"; }
}
private double factor = 1.0 / 9.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, 0, 0, 0, 0, 0, 0, 0, 1, },
{ 0, 0, 0, 0, 0, 0, 0, 1, 0, },
{ 0, 0, 0, 0, 0, 0, 1, 0, 0, },
{ 0, 0, 0, 0, 0, 1, 0, 0, 0, },
{ 0, 0, 0, 0, 1, 0, 0, 0, 0, },
{ 0, 0, 0, 1, 0, 0, 0, 0, 0, },
{ 0, 0, 1, 0, 0, 0, 0, 0, 0, },
{ 0, 1, 0, 0, 0, 0, 0, 0, 0, },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Soften Filter
The SoftenFilter can be used to smooth or soften an image. The matrix consists of 9 elements in a 3×3 configuration.

public class SoftenFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "SoftenFilter"; }
}
private double factor = 1.0 / 8.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 1, 1, 1, },
{ 1, 1, 1, },
{ 1, 1, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Sharpen Filters
Sharpening an image does not add additional detail to an image but rather adds emphasis to existing image details. Image sharpness is sometimes referred to as image crispness.
SharpenFilter
This filter is intended as a general usage sharpen filter. In a variety of scenarios this filter should provide a reasonable level of image sharpening depending on source image quality.

public class SharpenFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "SharpenFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -1, -1, },
{ -1, 9, -1, },
{ -1, -1, -1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Sharpen3x3Filter
The Sharpen3x3Filter results in a medium level of image sharpness, less intense when compared to the SharpenFilter discussed previously.

public class Sharpen3x3Filter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Sharpen3x3Filter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, -1, 0, },
{ -1, 5, -1, },
{ 0, -1, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Sharpen3x3FactorFilter
The Sharpen3x3FactorFilter provides a level of image sharpness similar to the Sharpen3x3Filter explored previously. Both filters define a 9 element 3×3 matrix. The filters differ in regards to Factor values. The Sharpen3x3Filter matrix values equate to a sum total of 1, the Sharpen3x3FactorFilter in contrast equate to a sum total of 3. The Sharpen3x3FactorFilter defines a Factor of 1 / 3, resulting in matrix sum total being negated to 1.

public class Sharpen3x3FactorFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Sharpen3x3FactorFilter"; }
}
private double factor = 1.0 / 3.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, -2, 0, },
{ -2, 11, -2, },
{ 0, -2, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Sharpen5x5Filter
The Sharpen5x5Filter matrix defines 25 elements in a 5×5 configuration. The level of image sharpness resulting from implementing this filter to a greater extent is depended on the source image. In some scenarios result images may appear slightly softened.

public class Sharpen5x5Filter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Sharpen5x5Filter"; }
}
private double factor = 1.0 / 8.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -1, -1, -1, -1, },
{ -1, 2, 2, 2, -1, },
{ -1, 2, 8, 2, 1, },
{ -1, 2, 2, 2, -1, },
{ -1, -1, -1, -1, -1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
IntenseSharpenFilter
The IntenseSharpenFilter produces result images with overly emphasized edge lines.

public class IntenseSharpenFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "IntenseSharpenFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 1, 1, 1, },
{ 1, -7, 1, },
{ 1, 1, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Edge Detection Filters
Edge detection is the first step towards feature detection and feature extraction in digital image processing. Edges are generally perceived in images in areas exhibiting sudden differences in brightness.
EdgeDetectionFilter
The EdgeDetectionFilter is intended to be used as a general purpose edge detection filter, considered appropriate in the majority of scenarios applied.

public class EdgeDetectionFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "EdgeDetectionFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -1, -1, },
{ -1, 8, -1, },
{ -1, -1, -1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
EdgeDetection45DegreeFilter
The EdgeDetection45DegreeFilter has the ability to detect edges at 45 degree angles more effectively than other edge detection filters.

public class EdgeDetection45DegreeFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "EdgeDetection45DegreeFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, 0, 0, 0, 0, },
{ 0, -2, 0, 0, 0, },
{ 0, 0, 6, 0, 0, },
{ 0, 0, 0, -2, 0, },
{ 0, 0, 0, 0, -1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
HorizontalEdgeDetectionFilter
The HorizontalEdgeDetectionFilter has the ability to detect horizontal edges more effectively than other edge detection filters.

public class HorizontalEdgeDetectionFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "HorizontalEdgeDetectionFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, 0, 0, 0, 0, },
{ 0, 0, 0, 0, 0, },
{ -1, -1, 2, 0, 0, },
{ 0, 0, 0, 0, 0, },
{ 0, 0, 0, 0, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
VerticalEdgeDetectionFilter
The VerticalEdgeDetectionFilter has the ability to detect vertical edges more effectively than other edge detection filters.

public class VerticalEdgeDetectionFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "VerticalEdgeDetectionFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 0, 0, -1, 0, 0, },
{ 0, 0, -1, 0, 0, },
{ 0, 0, 4, 0, 0, },
{ 0, 0, -1, 0, 0, },
{ 0, 0, -1, 0, 0, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
EdgeDetectionTopLeftBottomRightFilter
This filter closely resembles an embossed image indicating object depth whilst still providing a reasonable level of edge detection detail.

public class EdgeDetectionTopLeftBottomRightFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "EdgeDetectionTopLeftBottomRightFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 0.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -5, 0, 0, },
{ 0, 0, 0, },
{ 0, 0, 5, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Emboss Filters
Emboss filters produce result images with an emphasis on depth, based on lines/edges expressed in an input/source image. Result images give the impression of being three dimensional to a varying extent, depended on image details defined by input images.
EmbossFilter
The EmbossFilter is intended as a general application emboss filter. Take note of the Bias value of 128. Without a bias value, result images would be very dark or mostly black.

public class EmbossFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "EmbossFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 128.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { 2, 0, 0, },
{ 0, -1, 0, },
{ 0, 0, -1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Emboss45DegreeFilter
The Emboss45DegreeFilter has the ability to produce result images with good emphasis on 45 degree edges/lines.

public class Emboss45DegreeFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "Emboss45DegreeFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 128.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -1, 0, },
{ -1, 0, 1, },
{ 0, 1, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
EmbossTopLeftBottomRightFilter
The EmbossTopLeftBottomRightFilter provides a more subtle level of embossed result images.

public class EmbossTopLeftBottomRightFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "EmbossTopLeftBottomRightFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 128.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, 0, 0, },
{ 0, 0, 0, },
{ 0, 0, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
IntenseEmbossFilter
When implementing the IntenseEmbossFilter result images provide a good three dimensional/depth level. A drawback of this filter can sometimes be noticed in a reduction image detail.

public class IntenseEmbossFilter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "IntenseEmbossFilter"; }
}
private double factor = 1.0;
public override double Factor
{
get { return factor; }
}
private double bias = 128.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -1, -1, -1, 0, },
{ -1, -1, -1, 0, 1, },
{ -1, -1, 0, 1, 1, },
{ -1, 0, 1, 1, 1, },
{ 0, 1, 1, 1, 1, }, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
High Pass
High pass filters produce result images where only high frequency components are retained.

public class HighPass3x3Filter : ConvolutionFilterBase
{
public override string FilterName
{
get { return "HighPass3x3Filter"; }
}
private double factor = 1.0 / 16.0;
public override double Factor
{
get { return factor; }
}
private double bias = 128.0;
public override double Bias
{
get { return bias; }
}
private double[,] filterMatrix =
new double[,] { { -1, -2, -1, },
{ -2, 12, -2, },
{ -1, -2, -1,, };
public override double[,] FilterMatrix
{
get { return filterMatrix; }
}
}
Related Articles and Feedback
Feedback and questions are always encouraged. If you know of an alternative implementation or have ideas on a more efficient implementation please share in the comments section.
Dewald Esterhuizen
I’ve published a number of articles related to imaging and images of which you can find URL links here: