C# How to: Weighted Difference of Gaussians

Article Purpose

It is the purpose of this article to illustrate the concept of Difference of Gaussians Edge Detection. This article extends the conventional implementation of Difference of Gaussian algorithms through the application of equally sized matrix kernels only differing by a weight factor.

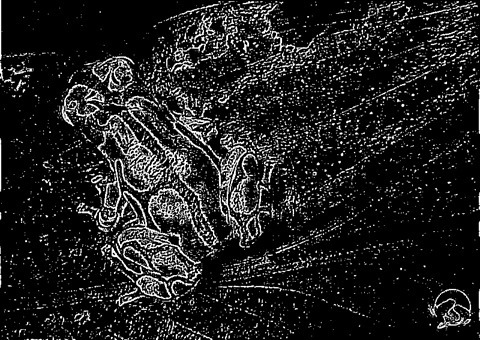
Frog: Kernel 5×5, Weight1 0.1, Weight2 2.1

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article relies on a sample application included as part of the accompanying sample source code. The sample application serves as a practical implementation of the concepts explored throughout this article.

The sample application user interface enables the user to configure and control the implementation of a Difference of Gaussians Edge Detection Image filter. The configuration options exposed through the sample application’s user interface can be detailed as follows:

Load/Save Images – When executing the sample application users are able to load source/input images from the local file system through clicking the Load Image button. If desired, the sample application enables users to save resulting images to the local file system through clicking the Save Image button.
Kernel Size – This option relates to the size of the matrix kernels that is to be implemented when performing Gaussian Blurring through image convolution. Smaller matrix kernels are faster to compute and generally result in image edges detected in the source/input image to be expressed through thinner gradient edges. Larger matrix kernels can be computationally expensive to compute as kernel sizes increase. In addition, the edges detected in source/input images will generally be expressed as thicker gradient edges in resulting images.
Weight Values – The sample application calculates Gaussian matrix kernels and in doing so implements a weight factor. A Weight Factor determines the blur intensity observed in result images after having applied image convolution. Higher weight factors result in a more intense level of Gaussian Blurring being applied. As expected, lower weight factors values result in a less intense level of Gaussian Blurring being applied. If the value of the first weight factor exceeds the value of the second weight factor resulting images will be generated with a Black background and edges being indicated in White. In a similar fashion, when the second weight factor value exceeds that of the first weight factor resulting images will be generated with a White background and edges being indicated in Black. The greater the difference between the first and second weight factor values result in a greater degree of image noise removal. When weight factor values only differ slightly, resulting images may be prone to image noise.

The following image is screenshot of the Weighted Difference of Gaussians sample application in action:

Frog: Kernel 5×5, Weight1 1.8, Weight2 0.1

Gaussian Blur

The Gaussian Blur algorithm can be described as one of the most popular and widely implemented methods of image blurring. From Wikipedia we gain the following excerpt:

A Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales.

Mathematically, applying a Gaussian blur to an image is the same as convolving the image with a Gaussian function. This is also known as a two-dimensional Weierstrass transform.

Take Note: The Gaussian Blur algorithm has the attribute of smoothing image detail/definition whilst also having an edge preservation attribute. When applying a Gaussian Blur to an image a level of image detail/definition will be blurred/smoothed away, done in a fashion that would exclude/preserve image gradient edges.

Frog: Kernel 5×5, Weight1 2.7, Weight2 0.1

Difference of Gaussians Edge Detection

Difference of Gaussian refers to a specific method of image edge detection. Difference of Gaussians, common abbreviated as DoG, functions through the implementation of Gaussian Image Blurring.

A clear and concise description can be found on the Difference of Gaussians Wikipedia Article Page:

In imaging science, difference of Gaussians is a feature enhancement algorithm that involves the subtraction of one blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing standard deviations. Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the difference of Gaussians is a band-pass filter that discards all but a handful of spatial frequencies that are present in the original grayscale image.

In a conventional sense Difference of Gaussians involves applying Gaussian Blurring to images created as copies of the original source/input image. There must be a difference in the size of the kernels implemented when applying image convolution. A typical example would be applying a 3×3 Gaussian blur on one image copy whilst applying a 5×5 Gaussian blur on another image copy. The final step requires creating a result image populated by subtracting the two blurred image copies. The results obtained from subtraction represents the edges forming part of the source/input image.

This article extends beyond the conventional method of implementing Difference of Gaussians Edge Detection. The implementation illustrated in this article retains the core concept of subtracting values which have been blurred to different intensities. The implementation method explored here differs from the conventional method in the sense that the matrix kernels implemented do not differ in size. Both matrix kernels are in fact required to have the same size dimensions.

The matrix kernels implemented are equal in terms of their size dimensions, although kernel values are different. Expressed from another angle: equally sized matrix kernels of which one represents a more intense level of blurring than the other. A matrix kernels’ resulting intensity can be determined by the weight factor implemented when calculating the kernel values.

Frog: Kernel 5×5, Weight1 3.7, Weight2 0.2

The advantages of implementing equally sized kernels can be described as follows:

Single Convolution implementation: Image Convolution involves executing several nested code loops. Application performance can be severely negatively impacted when executing large nested loops. The conventional method of implementing Difference of Gaussians generally involves having to implement two instances of image convolution, once per image copy. The Difference of Gaussians method implemented in this article executes the code loops related to image convolution only once. Considering the kernels are equal in size, both can be iterated within the same set of loops.

Eliminating Image subtraction: In conventional Difference of Gaussians implementations images expressing differing intensity levels of Gaussian Blurring have to be subtracted. The Difference of Gaussian implementation method described in this article eliminates the need to perform image subtraction. When applying image convolution using both kernels simultaneously the two results obtained, one from each kernel, can be subtracted and assigned to the result image. In addition, through calculating both kernel results at the same time further reduces the need to create two temporary source image copies.

Frog: Kernel 5×5, Weight1 2.4, Weight2 0.3

Difference of Gaussians Edge Detection Required Steps

When implementing a Difference of Gaussians Edge Detection several steps are required, those steps are detailed as follows:

Calculate Kernels – Before implementing image convolution two matrix kernels have to be calculated. The calculated kernels are required to be of equal size and differ in Gaussian Blur intensity. The sample application allows the user to configure kernel intensity through updating the weight values, expressed as Weight 1 and Weight 2.
Convert Source Image to Grayscale – Applying image convolution on grayscale images outperforms convolution on RGB images. When converting an RGB pixel to a grayscale pixel, colour components are combined to form a single gray level intensity. In other words a grayscale image consists of a third of the number of pixels when compared to the RGB image from which the grayscale image had been rendered. In the case of an ARGB image the derived grayscale image will be expressed in 25% of the number of pixels forming part of the source ARGB image. When applying image convolution the number of processor cycles increases when the image pixel count increases.
Perform Convolution Implementing Thresholds – Using the newly created grayscale image perform image convolution for both kernels calculated in the first step. The result value equates to subtracting the two results obtained from convolution. If the result value exceeds the difference between the first and second kernel weight value, the resulting pixel should be set to White, if not, set the result pixel to Black.

Frog: Kernel 5×5, Weight1 2.1, Weight2 0.5

Calculating Gaussian Convolution Kernels

The sample application implements Gaussian Blur Kernel calculations. The matrix kernels implemented in image convolution are calculated at runtime, as opposed to being hard coded. Being able to dynamically construct convolution kernels has the advantage of providing a greater degree of control in runtime regarding image convolution application.

Several steps are involved in calculating Gaussian Blur Matrix Kernels. The first required step being to determine the Matrix Kernel Size and Weight. The size and weight factor of a matrix kernel comprises the two configurable values implemented when calculating Gaussian Blur Kernels. In the case of this article and the sample application those values will be configured by the user through the sample application’s user interface.

The formula implemented in calculating Gaussian Blur Kernels can be expressed as follows:

The formula contains a number of symbols, which define how the filter will be implemented. The symbols forming part of the Gaussian Kernel formula are described in the following list:

G(x y) – A value calculated using the Gaussian Kernel formula. This value forms part of a Kernel, representing a single element.
π – Pi, one of the better known members of the Greek alphabet. The mathematical constant defined as 22 / 7.
σ – The lower case version of the Greek alphabet letter Sigma. This symbol simply represents a threshold or factor value, as specified by the user.
e – The formula references a lower case e symbol. The symbol represents Euler’s number. The value of Euler’s number has been defined as a mathematical constant equating to 2.71828182846.
x, y – The variables referenced as x and y relate to pixel coordinates within an image. y Representing the vertical offset or row and x represents the horizontal offset or column.

Note: The formula’s implementation expects x and y to equal zero values when representing the coordinates of the pixel located in the middle of the kernel.

Frog: Kernel 7×7, Weight1 0.1, Weight2 2.0

Implementing Gaussian Kernel Calculations

The sample application defines the GaussianCalculator.Calculate method. This method accepts two parameters, kernel size and kernel weight. The following code snippet details the implementation:

public static double[,] Calculate(int lenght, double weight) 
{
    double[,] Kernel = new double [lenght, lenght]; 
    double sumTotal = 0; 

  
    int kernelRadius = lenght / 2; 
    double distance = 0; 

  
    double calculatedEuler = 1.0 /  
    (2.0 * Math.PI * Math.Pow(weight, 2)); 

  
    for (int filterY = -kernelRadius; 
         filterY <= kernelRadius; filterY++) 
    {
        for (int filterX = -kernelRadius; 
            filterX <= kernelRadius; filterX++) 
        {
            distance = ((filterX * filterX) +  
                       (filterY * filterY)) /  
                       (2 * (weight * weight)); 

  
            Kernel[filterY + kernelRadius,  
                   filterX + kernelRadius] =  
                   calculatedEuler * Math.Exp(-distance); 

  
            sumTotal += Kernel[filterY + kernelRadius,  
                               filterX + kernelRadius]; 
        } 
    } 

  
    for (int y = 0; y < lenght; y++) 
    { 
        for (int x = 0; x < lenght; x++) 
        { 
            Kernel[y, x] = Kernel[y, x] *  
                           (1.0 / sumTotal); 
        } 
    } 

  
    return Kernel; 
}

Frog: Kernel 3×3, Weight1 0.1, Weight2 1.8

Implementing Difference of Gaussians Edge Detection

The sample source code defines the DifferenceOfGaussianFilter method. This method has been defined as an extension method targeting the Bitmap class. The following code snippet provides the implementation:

public static Bitmap DifferenceOfGaussianFilter(this Bitmap sourceBitmap,  
                                                int matrixSize, double weight1, 
                                                double weight2) 
{
    double[,] kernel1 =  
    GaussianCalculator.Calculate(matrixSize,  
    (weight1 > weight2 ? weight1 : weight2)); 

 
    double[,] kernel2 =  
    GaussianCalculator.Calculate(matrixSize,  
    (weight1 > weight2 ? weight2 : weight1)); 

 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly, 
                                         PixelFormat.Format32bppArgb); 

 
    byte[] pixelBuffer = new byte [sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte [sourceData.Stride * sourceData.Height]; 
    byte[] grayscaleBuffer = new byte [sourceData.Width * sourceData.Height]; 

 
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 

 
    double rgb = 0; 

 
    for (int source = 0, dst = 0;  
         source < pixelBuffer.Length && dst < grayscaleBuffer.Length;  
         source += 4, dst++) 
    { 
        rgb = pixelBuffer * 0.11f; 
        rgb += pixelBuffer * 0.59f; 
        rgb += pixelBuffer * 0.3f; 

 
        grayscaleBuffer[dst] = (byte)rgb; 
    }

 
    double color1 = 0.0; 
    double color2 = 0.0; 

 
    int filterOffset = (matrixSize - 1) / 2; 
    int calcOffset = 0; 

 
    for (int source = 0, dst = 0;  
         source < grayscaleBuffer.Length && dst + 4 < resultBuffer.Length;  
         source++, dst += 4) 
    { 
        color1 = 0; 
        color2 = 0; 

         
        for (int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++) 
        {
            for (int filterX = -filterOffset; 
                filterX <= filterOffset; filterX++) 
            {
                calcOffset = source + (filterX) + 
                             (filterY * sourceBitmap.Width); 

 
                calcOffset = (calcOffset < 0 ? 0 :  
                             (calcOffset >= grayscaleBuffer.Length ?  
                             grayscaleBuffer.Length - 1 : calcOffset)); 

 
                color1 += (grayscaleBuffer[calcOffset]) * 
                           kernel1[filterY + filterOffset, 
                           filterX + filterOffset]; 

 
                color2 += (grayscaleBuffer[calcOffset]) * 
                           kernel2[filterY + filterOffset, 
                           filterX + filterOffset]; 
            } 
        }

 
        color1 = color1 - color2; 
        color1 = (color1 >= weight1 - weight2 ? 255 : 0); 

 
        resultBuffer[dst] = (byte)color1; 
        resultBuffer[dst + 1] = (byte)color1; 
        resultBuffer[dst + 2] = (byte)color1; 
        resultBuffer[dst + 3] = 255; 
    }

 
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 

 
    BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 

 
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

 
    return resultBitmap; 
}

Frog: Kernel 3×3, Weight1 2.1, Weight2 0.7

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following image files feature as sample images:

Panamanian Golden Frog – Licensed under the Creative Commons Attribution 2.0 Generic license. Attribution: Brian Gratwicke. Download from Wikipedia.
Dendropsophus Microcephalus – Licensed under the Creative Commons Attribution 2.0 Generic license. Attribution: Brian Gratwicke. Download from Wikipedia.
Tyler’s Tree Frog – Has been released into the public domain by its author, LiquidGhoul. This applies worldwide. Download from Wikipedia.
Mimic Poison Frog – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from Wikipedia.
Phyllobates Terribilis – This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Germany license. Attribution: Wilfried Berns. Download from Wikipedia.

Panamanian Golden Frog

Dendropsophus Microcephalus

Tyler’s Tree Frog

Mimic Poison Frog

Phyllobates Terribilis

Software by Default