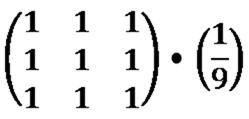Blur | Software by Default

Posts Tagged 'Blur'

C# How to: Min/Max Edge Detection

Article Purpose

This article serves as a detailed discussion on implementing image edge detection through pixel neighbourhood maximum and minimum value subtraction. Additional concepts illustrated in this article include implementing a median filter and RGB grayscale conversion.

Frog Filter 3×3 Smoothed

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article’s accompanying sample source code includes a Windows Forms based sample application. The sample application provides an implementation of the concepts explored by this article. Concepts discussed can be easily replicated and tested by using the sample application.

Source/input image files can be specified from the local file system when clicking the Load Image button. Additionally users also have the option to save resulting filtered images by clicking the Save Image button.

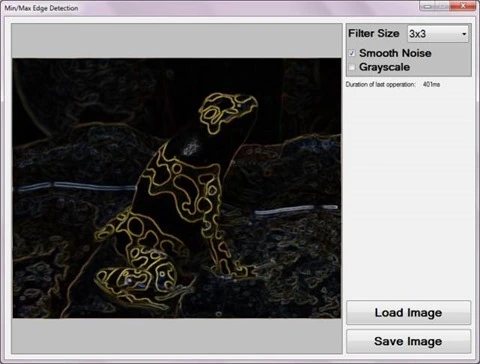
The sample application user interface enables the user to specify three filter configuration values. These values serve as input parameters to the Min/Max Edge Detection Filter and can be described as follows:

Filter Size – Determines the number of surrounding pixels to consider when calculating the minimum and maximum pixel values. This value equates to the size of a pixel’s neighbourhood of pixels. When gradient edges expressed in a source image requires a higher or lower level of expression in result images the filter size value should be adjusted. Higher Filter Size values result in gradient edges being expressed at greater intensity levels in resulting images. Inversely, lower Filter Size values delivers the opposite result of gradient edges being expressed at lesser intensity levels.
Smooth Noise – Image noise when present in source images, can to varying degrees affect the Min/Max Edge Detection Filter’s accuracy in calculating gradient edges. In order to reduce the negative affects of source image noise an image smoothing filter may be implemented. Smoothing out image noise requires additional filter processing and therefore requires additional computation time. If source images reflect minor or no image noise, additional image smoothing may be excluded to reduce filter processing duration.
Grayscale – When required, result images can be expressed in grayscale through configuring this value.

The following image represents a screenshot of the Min/Max Edge Detection Sample application in action.

Min/Max Edge Detection

The method of edge detection illustrated in this article can be classified as a variation of commonly implemented edge detection methods. Image edges expressed within a source image can be determined through the presence of sudden and significant changes in gradient levels that occur within a small/limited perimeter.

As a means to determine gradient level changes the Min/Max Edge Detection algorithm performs pixel neighbourhood inspection, comparing maximum and minimum colour channel values. Should the difference between maximum and minimum colour values be significant, it would be an indication of a significant change in gradient level within the pixel neighbourhood being inspected.

Image noise represents interference in relation to regular gradient level expression. Image noise does not signal the presence of an image edge, although could potentially result in incorrectly determining image edge presence. Image noise and the negative impact thereof can be significantly reduced when applying image smoothing, also sometimes referred to as image blur. The Min/Max Edge Detection algorithm makes provision for optional image smoothing implemented in the form of a median filter.

The following sections provide more detail regarding the concepts introduced in this section, pixel neighbourhood and median filter.

Frog Filter 3×3 Smoothed

Pixel Neighbourhood

A pixel neighbourhood refers to a set of pixels, all of which are related through pixel location coordinates. The width and height of a pixel neighbourhood must be equal, in other words, a pixel neighbourhood can only be square. Additionally, the width/height of a pixel neighbourhood must be an uneven value. When inspecting a pixel’s neighbouring pixels, the pixel being inspected will always be located at the exact center of the pixel neighbourhood. Only when a pixel neighbourhood’s width/height are an uneven value can such a pixel neighbourhood have an exact center pixel. Each pixel represented in an image has a different set of neighbours, some neighbours overlap, but no two pixels have the exact same neighbours. A pixel’s neighbouring pixels can be determined when considering the pixel to be at the center of a block of pixels, extending half the neighbourhood size less one in horizontal, vertical and diagonal directions.

Median Filter

In context of this article and the Min/Max Edge Detection filter, median filtering has been implemented as a means to reduce source image noise. From the Median Wikipedia page we gain the following quote:

In statistics and probability theory, the median is the number separating the higher half of a data sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one (e.g., the median of {3, 3, 5, 9, 11} is 5).

Frog Filter 3×3 Smoothed

The application of a median filter is based in the concept of pixel neighbourhood as discussed earlier. The implementation steps required when applying a median filter can be described as follows:

Iterate every pixel. The pixel neighbourhood of each pixel in a source image needs to be determined and inspected.
Order/Sort pixel neighbourhood values. Once a pixel neighbourhood for a specific pixel has been determined the values expressed by all the pixels in that neighbourhood needs to be sorted or ordered according to value.
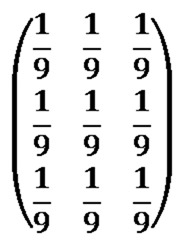
Determine midpoint value. In relation to the sorted pixel neighbourhood values, the value positioned exactly halfway between first and last value needs to be determined. As an example, if a pixel neighbourhood contains a total of nine pixels, the midpoint would be at position number five, which is four positions from the first and last value inclusive. The midpoint value in a sorted range of neighbourhood pixel values, is the median value of that pixel neighbourhood’s values.

The median filter should not be confused with the mean filter. A median will always be a midpoint value from a sorted value range, whereas a mean value is equal to the calculated average of a value range. The median filter has the characteristic of reducing image noise whilst still preserving image edges. The mean filter will also reduce image noise, but will do so through generalized image blurring, also referred to as box blur, which does not preserve image edges.

Note that when applying a median filter to RGB colour images median values need to be determined per individual colour channel.

Frog Filter 3×3 Smoothed

Min/Max Edge Detection Algorithm

Image edge detection based in a min/max approach requires relatively few steps, which can be combined in source code implementations to be more efficient from a computational/processing perspective. A higher level logical definition of the steps required can be described as follows:

Image Noise Reduction – If image noise reduction is required apply a median filter to the source image.
Iterate through all of the pixels contained within an image.
For each pixel being iterated, determine the neighbouring pixels. The pixel neighbourhood size will be determined by the specified filter size.
Determine the Minimum and Maximum pixel value expressed within the pixel neighbourhood.
Subtract the Minimum from the Maximum value and assign the result to the pixel currently being iterated.
Apply Grayscale conversion to the pixel currently being iterated, only if grayscale conversion had been configured.

Implementing a Min/Max Edge Detection Filter

The source code implementation of the Min/Max Edge Detection Filter declares two methods, a median filter method and an edge detection method. A median filter and edge detection filter cannot be processed simultaneously. When applying a median filter, the median value of a pixel neighbourhood determined from a source image should be expressed in a separate result image. The original source image should not be altered whilst inspecting pixel neighbourhoods and calculating median values. Only once all pixel values in the result image has been set, can the result image serve as a source image to an edge detection filter method.

The following code snippet provides the source code definition of the MedianFilter method.

private static byte[] MedianFilter(this byte[] pixelBuffer,
                                    int imageWidth,
                                    int imageHeight,
                                    int filterSize)
{
    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;

    int byteOffset = 0;
    var neighbourCount = filterSize * filterSize;
    int medianIndex = neighbourCount / 2;

    var blueNeighbours = new byte[neighbourCount];
    var greenNeighbours = new byte[neighbourCount];
    var redNeighbours = new byte[neighbourCount];

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            for (int filterY = -filterOffset, neighbour = 0;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++, neighbour++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    blueNeighbours[neighbour] = pixelBuffer[calcOffset];
                    greenNeighbours[neighbour] = pixelBuffer[calcOffset + greenOffset];
                    redNeighbours[neighbour] = pixelBuffer[calcOffset + redOffset];
                }
            }

            Array.Sort(blueNeighbours);
            Array.Sort(greenNeighbours);
            Array.Sort(redNeighbours);

            resultBuffer[byteOffset] = blueNeighbours[medianIndex];
            resultBuffer[byteOffset + greenOffset] = greenNeighbours[medianIndex];
            resultBuffer[byteOffset + redOffset] = redNeighbours[medianIndex];
            resultBuffer[byteOffset + alphaOffset] = maxByteValue;
        }
    }

    return resultBuffer;
}

Notice the definition of three separate byte arrays, each intended to represent a pixel neighbourhood’s pixel values related to a specific colour channel. Each neighbourhood colour channel byte array needs to be sorted according to value. The value located at the array index exactly halfway from the start and the end of the array represents the median value. When a median value has been determined, the result buffer pixel related to the source buffer pixel in terms of XY Location needs to be set.

Frog Filter 3×3 Smoothed

The sample source code defines two overloaded versions of an edge detection method. The first version is defined as an extension method targeting the Bitmap class. A FilterSize parameter is the only required parameter, intended to specify pixel neighbourhood width/height. In addition, when invoking this method optional parameters may be specified. When image noise reduction should be implemented the smoothNoise parameter should be defined as true. If resulting images are required in grayscale the last parameter, grayscale, should reflect true. The following code snippet provides the definition of the MinMaxEdgeDetection method.

public static Bitmap MinMaxEdgeDetection(this Bitmap sourceBitmap,
                                            int filterSize, 
                                            bool smoothNoise = false, 
                                            bool grayscale = false)
{
    return sourceBitmap.ToPixelBuffer()
                        .MinMaxEdgeDetection(sourceBitmap.Width, 
                                            sourceBitmap.Height, 
                                            filterSize,
                                            smoothNoise,
                                            grayscale)
                        .ToBitmap(sourceBitmap.Width, 
                                    sourceBitmap.Height);
}

The MinMaxEdgeDetection method as expressed above essentially acts as a wrapper method, invoking the overloaded version of this method, performing mapping between Bitmap objects and byte array pixel buffers.

An overloaded version of the MinMaxEdgeDetection method performs all of the tasks required in edge detection through means of minimum maximum pixel neighbourhood value subtraction. The method definition as provided by the following code snippet.

private static byte[] MinMaxEdgeDetection(this byte[] sourceBuffer,
                                          int imageWidth,
                                          int imageHeight,
                                          int filterSize,
                                          bool smoothNoise = false,
                                          bool grayscale = false)
{
    byte[] pixelBuffer = sourceBuffer;

    if (smoothNoise)
    {
        pixelBuffer = sourceBuffer.MedianFilter(imageWidth, 
                                                imageHeight, 
                                                filterSize);
    }

    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;

    int byteOffset = 0;

    byte minBlue = 0, minGreen = 0, minRed = 0;
    byte maxBlue = 0, maxGreen = 0, maxRed = 0;

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            minBlue = maxByteValue;
            minGreen = maxByteValue;
            minRed = maxByteValue;

            maxBlue = minByteValue;
            maxGreen = minByteValue;
            maxRed = minByteValue;

            for (int filterY = -filterOffset;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    minBlue = Math.Min(pixelBuffer[calcOffset], minBlue);
                    maxBlue = Math.Max(pixelBuffer[calcOffset], maxBlue);

                    minGreen = Math.Min(pixelBuffer[calcOffset + greenOffset], minGreen);
                    maxGreen = Math.Max(pixelBuffer[calcOffset + greenOffset], maxGreen);

                    minRed = Math.Min(pixelBuffer[calcOffset + redOffset], minRed);
                    maxRed = Math.Max(pixelBuffer[calcOffset + redOffset], maxRed);
                }
            }

            if (grayscale)
            {
                resultBuffer[byteOffset] = ByteVal((maxBlue - minBlue) * 0.114 + 
                                                    (maxGreen - minGreen) * 0.587 + 
                                                    (maxRed - minRed) * 0.299);

                resultBuffer[byteOffset + greenOffset] = resultBuffer[byteOffset];
                resultBuffer[byteOffset + redOffset] = resultBuffer[byteOffset];
                resultBuffer[byteOffset + alphaOffset] = maxByteValue;
            }
            else
            {
                resultBuffer[byteOffset] = (byte)(maxBlue - minBlue);
                resultBuffer[byteOffset + greenOffset] = (byte)(maxGreen - minGreen);
                resultBuffer[byteOffset + redOffset] = (byte)(maxRed - minRed);
                resultBuffer[byteOffset + alphaOffset] = maxByteValue;
            }
        }
    }

    return resultBuffer;
}

As discussed earlier, image noise reduction if required should be the first task performed. Based on parameter value the method applies a median filter to the source image buffer.

When iterating a pixel neighbourhood a comparison is performed between the currently iterated neighbouring pixel’s value and the previously determined minimum and maximum values.

When the grayscale method parameter reflects true, a grayscale algorithm is applied to the difference between the determined maximum and minimum pixel neighbourhood values.

Should the grayscale method parameter reflect false, grayscale algorithm logic will not execute. Instead, the result obtained from subtracting the determined minimum and maximum values are assigned to the relevant pixel and colour channel on the result buffer image.

Frog Filter 3×3 Smoothed

Sample Images

This article features several sample images provided as examples. All sample images were created using the sample application. All of the original source images used in generating sample images have been licensed by their respective authors to allow for reproduction here. The following section lists each original source image and related license and copyright details.

C# How to: Standard Deviation Edge Detection

Published August 8, 2015 C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Arithmetic , Image Filtering , Image Filters , Image Processing , Opensource Leave a Comment
Tags: Alpha Red Green Blue, Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, C#, Code Sample, Color Filters, Computer vision, Converting Images, Edge Detection, Extension Methods, Graphic Filters, How to, Image, Image Intensity, Image Manipulation, Image processing, Image Transform, Machine vision, Median Filter, Pixel Filters, Standard Deviation

Article Purpose

This article explores image edge detection implemented through computing pixel neighbourhood standard deviation on RGB colour images. The main sections of this article consists of a detailed explanation of the concepts related to the standard deviation edge detection algorithm and an in-depth discussion and a practical implementation through source code.

Butterfly Filter 3×3 Factor 5.0

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample application user interface exposes three filter configuration values to the end user in the form of predefined filter size values, a grayscale output flag and a variance factor. End users can configure whether filtered result images should express image edges using source image colour values or in grayscale. The filter size value specified by the user determines the number of pixels included when calculating standard deviation values.

Filter size has a direct correlation to the extend at which gradient edges will be represented in resulting images. Faint edge values require larger filter size values in order to be expressed in a resulting output image. Larger filter size values require additional computation and would thus have a longer completion time when compared to smaller filter size values.

The following screenshot captures the Standard Deviation Edge Detection sample application in action.

Standard Deviation Edge Detection

Image edge detection can be achieved through a variety of methods, each associated with particular benefits and trade offs. This article is focussed on image edge detection through implementing standard deviation calculations on a pixel neighbourhood.

Pixel Neighbourhood

Butterfly Filter 3×3 Factor 5

Pixel Neighbourhood Mean value

Mean value calculation forms a core part in calculating standard deviation. The mean value from a set of values could be considered equivalent to the value set’s average value. The average of a set of values can be calculated as the sum total of all the values in a set, divided by the number of values in the set.

Standard Deviation

From the Standard Deviation Wikipedia page we gain the following quote:

In statistics, the standard deviation (SD, also represented by the Greek letter sigma, σ for the population standard deviation or s for the sample standard deviation) is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A standard deviation close to 0 indicates that the data points tend to be very close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values

A pixel neighbourhood’s standard deviation can indicate whether a significant change in image gradient is present in a pixel neighbourhood. A large standard deviation value is an indication that the neighbourhood’s pixel values could be spread far from the calculated mean. Inversely, a small standard deviation will indicate that the neighbourhood’s pixel values are closer to the calculated mean. A sudden change in image gradient will equate to a large standard deviation.

Steps required in calculating standard deviation can be described as follows:

Calculate the Mean value. Calculate the sum of all pixels in a pixel neighbourhood then divide the sum total using the number of pixels contained in a neighbourhood. In essence calculating the mean value should be seen as calculating the average of all the pixels in a neighbourhood.
Calculate combined Variance using Mean value. Subtract the mean value from each pixel in the neighbourhood, the result should be squared and added to a sum total. Variance should then be calculated as the calculated mean subtracted squared pixel value divided using the number of pixels in a neighbourhood.
Calculate standard deviation as the Variance square root.

Butterfly Filter 3×3 Factor 5

Standard Deviation Edge Detection Algorithm

The standard deviation edge detection algorithm is based in the concept of standard deviation, providing additional capabilities. The algorithm allows for a more prominent expression of variance through means of a variance factor. Calculated variance values can be increased or decreased when implementing a variance factor. When variances are less significant, resulting images will express gradient edges at faint/low intensity levels. Providing a variance factor will result in output images expressing gradient edges at a higher intensity.

Variance factor and filter size should not be confused. When source gradient edges are expressed at low intensities, higher filter sizes would result in those low intensity source edges to be expressed in resulting images. In a scenario where high intensity gradient edges from a source image are expressed in resulting images at low intensities, a higher variance factor would increase resulting image gradient edge intensity.

The following list provides a summary of the steps required to implement the standard deviation edge detection algorithm:

Iterate through all of the pixels contained within an image.
For each pixel being iterated, determine the neighbouring pixels. The pixel neighbourhood size will be determined by the specified filter size.
Calculate the Mean value of the current pixel neighbourhood.
Calculate the Variance. Subtract the Mean value from each neighbourhood pixel, the result should be squared and summed to a variance total value. Finally, the variance total value should be divided by the number of pixels that make up the pixel neighbourhood. If a variance factor had been specified, the calculated variance value should be multiplied against it and the result assigned as the new calculated variance value.
Calculate the Standard Deviation. Once the variance has been calculated the standard deviation can be expressed as the square root of the calculated variance value. The standard deviation value should be assigned to the result buffer pixel relating to the source buffer pixel currently being iterated.

It is important to note that the steps as described above should be applied per individual colour channel, Red, Green and Blue.

Butterfly Filter 3×3 Factor 4.5

Implementing a Standard Deviation Edge Detection filter

The sample source code that accompanies this article provides a public extension method targeting the Bitmap class. A private overloaded implementation of the StandardDeviationEdgeDetection method performs the bulk of the required functionality. The following code snippet illustrates the public overloaded version of the StandardDeviationEdgeDetection method:

public static Bitmap StandardDeviationEdgeDetection(this Bitmap sourceBuffer, 
                                                    int filterSize, 
                                                    float varianceFactor = 1.0f, 
                                                    bool grayscaleOutput = true)
{
     return sourceBuffer.ToPixelBuffer()
                        .StandardDeviationEdgeDetection(sourceBuffer.Width, 
                                                        sourceBuffer.Height,
                                                        filterSize,
                                                        varianceFactor,
                                                        grayscaleOutput)
                         .ToBitmap(sourceBuffer.Width, sourceBuffer.Height);
}

The StandardDeviationEdgeDetection method accepts 3 parameters, the first Bitmap parameter serves to signal that the method is an extension method targeting the Bitmap class. A brief description of the other parameters as follows:

filterSize determines the pixel neighbourhood size. Note that the parameter is expected to reflect the pixel neighbourhood width/height. As an example, a filterSize parameter value provided as 3 would equate to a pixel neighbourhood consisting of 9 pixels, as would a filterSize of 5 indicate a neighbourhood of 25 pixels.
varianceFactor signifies the factor value applied to a calculated variance.
grayscale being a boolean value indicates whether the resulting image should be represented in grayscale, or in the original colour values from the source image.

Butterfly Filter 3×3 Factor 4

The following code snippet relates the private implementation of the StandardDeviationEdgeDetection method, which performs all of the tasks required to implement the standard deviation edge detection algorithm.

private static byte[] StandardDeviationEdgeDetection(this byte[] pixelBuffer, 
                                                     int imageWidth, 
                                                     int imageHeight,
                                                     int filterSize,
                                                     float varianceFactor = 1.0f,
                                                     bool grayscaleOutput = true)
{
    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;
            
    int byteOffset = 0;
    var neighbourCount = filterSize * filterSize;
            
    var blueNeighbours = new int[neighbourCount];
    var greenNeighbours = new int[neighbourCount];
    var redNeighbours = new int[neighbourCount];

    double resetValue = 0;
    double meanBlue = 0, meanGreen = 0, meanRed = 0;
    double varianceBlue = 0, varianceGreen = 0, varianceRed = 0;

    varianceFactor = varianceFactor * varianceFactor;

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            meanBlue = resetValue;
            meanGreen = resetValue;
            meanRed = resetValue;

            varianceBlue = resetValue;
            varianceGreen = resetValue;
            varianceRed = resetValue;

            for (int filterY = -filterOffset, neighbour = 0;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++, neighbour++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    blueNeighbours[neighbour] = pixelBuffer[calcOffset];
                    greenNeighbours[neighbour] = pixelBuffer[calcOffset + 1];
                    redNeighbours[neighbour] = pixelBuffer[calcOffset + 2];
                }
            }

            meanBlue = blueNeighbours.Average();
            meanGreen = greenNeighbours.Average();
            meanRed = redNeighbours.Average();

            for (int n = 0; n < neighbourCount; n++)
            {
                varianceBlue = varianceBlue + 
                                SquareNumber(blueNeighbours[n] - meanBlue);
                varianceGreen = varianceGreen + 
                                SquareNumber(greenNeighbours[n] - meanGreen);
                varianceRed = varianceRed + 
                                SquareNumber(redNeighbours[n] - meanRed);
            }

            varianceBlue = varianceBlue / 
                            neighbourCount * 
                            varianceFactor;

            varianceGreen = varianceGreen /
                            neighbourCount * 
                            varianceFactor;

            varianceRed = varianceRed / 
                            neighbourCount * 
                            varianceFactor;

            if (grayscaleOutput)
            {
                var pixelValue = ByteVal(ByteVal(Math.Sqrt(varianceBlue)) |
                                         ByteVal(Math.Sqrt(varianceGreen)) | 
                                         ByteVal(Math.Sqrt(varianceRed)));

                resultBuffer[byteOffset] = pixelValue;
                resultBuffer[byteOffset + 1] = pixelValue;
                resultBuffer[byteOffset + 2] = pixelValue;
                resultBuffer[byteOffset + 3] = Byte.MaxValue;
            }
            else
            {
                resultBuffer[byteOffset] = ByteVal(Math.Sqrt(varianceBlue));
                resultBuffer[byteOffset + 1] = ByteVal(Math.Sqrt(varianceGreen));
                resultBuffer[byteOffset + 2] = ByteVal(Math.Sqrt(varianceRed));
                resultBuffer[byteOffset + 3] = Byte.MaxValue;
            }
        }
    }

    return resultBuffer;
}

This method features several for loops, resulting in each image pixel being iterated. Notice how the two inner most loops declare negative initializer values. In order to determine a pixel’s neighbourhood, the pixel should be considered as being located at the exact center of the neighbourhood. Negative initializer values enable the code to determine neighbouring pixels located to the left and above of the pixel being iterated.

A pixel neighbourhood needs to be determined in terms of each colour channel, Red, Green and Blue. The pixel neighbourhood of each colour channel must be averaged individually. Logically it follows that pixel neighbourhood variance should also be calculated per colour channel.

The method signature indicates the varianceFactor parameter should be optional and assigned a default value of 1.0. Should a variance factor not be required, implementing a default factor value of 1.0 will not result in any change to the calculated variance value.

When grayscale output has been configured the resulting output pixel will express the same value on all three colour channels. The grayscale value will be calculated through the application of a bitwise OR operation, applied to the standard deviation of each colour channel. The square root of a pixel neighbourhood’s variance provides the standard deviation value for that pixel neighbourhood.

If grayscale output had not been configured the resulting pixel colour channels will be assigned the standard deviation of the related colour channel on the source pixel.

private const byte maxByteValue = Byte.MaxValue;
private const byte minByteValue = Byte.MinValue;

public static byte ByteVal(int val)
{
    if (val < minByteValue) { return  minByteValue; }
    else if (val > maxByteValue) { return  maxByteValue; }
    else { return (byte)val; }
}

The StandardDeviationEdgeDetection method reflects several references to the ByteVal method, as illustrated in the code snippet above. Casting double and int values to byte values could result in values exceeding the upper and lower bounds allowed by the byte type. The ByteVal method tests whether a value would exceed upper and lower bounds, when determined to do so the resulting value is assigned either the upper inclusive bound or lower inclusive bound value, depending on the bound being exceeded.

Bee Filter 3×3 Factor 5

Sample Images

C# How to: Image Distortion Blur

Published August 9, 2013 Augmented Reality , Blogging , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Filters , Image Processing , Image Transform , Microsoft , New Version , Non-Photorealistic Rendering , Opensource , Tip , Update Leave a Comment
Tags: Alpha Red Green Blue, Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, C#, Code Sample, Color Filters, Computer vision, Converting Images, Extension Methods, Graphic Filters, How to, Image, Image Blur, Image Distortion, Image Intensity, Image Manipulation, Image processing, Image Transform, Machine vision, Median Filter, Morphologial Filters, Non-Photorealistic Rendering, Pixel Filters

Article Purpose

This article explores the process of implementing an Image Distortion Blur filter. This image filter is classified as a non-photo realistic image filter, primarily implemented in rendering artistic effects.

Flower: Distortion Factor 15

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Flower: Distortion Factor 10

Using the Sample Application

The sample source code that accompanies this article includes a Windows Forms based sample application. The concepts explored in this article have all been implemented as part of the sample application. From an end user perspective the following configurable options are available:

Load/Save Images – Clicking the Load Image button allows a user to specify a source/input image. If desired, output filtered images can be saved to the local file system by clicking the Save Image button.
Distortion Factor – The level or intensity of image distortion applied when implementing the filter can be specified when adjusting the Distortion Factor through the user interface. Lower factor values result in less distortion being evident in resulting images. Specifying higher factor values result in more intense image distortion being applied.

The following image is screenshot of the Image Distortion Blur sample application:

Flower: Distortion Factor 10

Flower: Distortion Factor 10

Image Distortion

In this article and the accompanying sample source code images are distorted through slightly adjusting each individual pixel’s coordinates. The direction and distance by which pixel coordinates are adjusted differ per pixel as a result of being randomly selected. The maximum distance offset applied depends on the user specified Distortion Factor. Once all pixel coordinates have been updated, implementing a Median Filter provides smoothing and an image blur effect.

Applying an Image Distortion Filter requires implementing the following steps:

Iterate Pixels – Each pixel forming part of the source/input image should be iterated.
Calculate new Coordinates – For every pixel being iterated generate two random values representing XY-coordinate offsets to be applied to a pixel’s current coordinates. Offset values can equate to less than zero in order to represent coordinates above or to the left of the current pixel.
Apply Median Filter – The newly offset pixels will appear somewhat speckled in the resulting image. Applying a Median Filter reduces the speckled appearance whilst retaining a distortion effect.

Flower: Distortion Factor 10

Median Filter

Applying a Median Filter is the final step required when implementing an Image Distortion Blur filter. Median Filters are often implemented in reducing image noise. The method of image distortion illustrated in this article express similarities when compared to image noise. In order to soften the appearance of image noise we implement a Median Filter.

A Median Filter can be applied through implementing the following steps:

Iterate Pixels – Each pixel forming part of the source/input image should be iterated.
Inspect Pixel Neighbourhood – Each neighbouring pixel in relation to the pixel currently being iterated should be added to a temporary collection.
Determine Neighbourhood Median – Once all neighbourhood pixels have been added to a temporary collection, sort the collection by value. The element value located at the middle of the collection represents the pixel neighbourhood’s Median value.

Flower: Distortion Factor 10

Flower: Distortion Factor 15

Implementing Image Distortion

The sample source code defines the DistortionBlurFilter method, an extension method targeting the Bitmap class. The following code snippet illustrates the implementation:

public static Bitmap DistortionBlurFilter( 
         this Bitmap sourceBitmap, int distortFactor) 
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = sourceBitmap.GetByteArray(); 

 
    int imageStride = sourceBitmap.Width * 4; 
    int calcOffset = 0, filterY = 0, filterX = 0; 
    int factorMax = (distortFactor + 1) * 2; 
    Random rand = new Random(); 

 
    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    {
        filterY = distortFactor - rand.Next(0, factorMax); 
        filterX = distortFactor - rand.Next(0, factorMax); 

 
        if (filterX * 4 + (k % imageStride) < imageStride  
                   && filterX * 4 + (k % imageStride) > 0) 
        { 
            calcOffset = k + filterY * imageStride +  
                         4 * filterX; 

 
            if (calcOffset >= 0 &&  
                calcOffset + 4 < resultBuffer.Length) 
            { 
                resultBuffer[calcOffset] = pixelBuffer[k]; 
                resultBuffer[calcOffset + 1] = pixelBuffer[k + 1]; 
                resultBuffer[calcOffset + 2] = pixelBuffer[k + 2]; 
            }
        }
    }

 
    return resultBuffer.GetImage(sourceBitmap.Width,  
                        sourceBitmap.Height).MedianFilter(3); 
}

Flower: Distortion Factor 15

Implementing a Median Filter

The MedianFilter extension method targets the Bitmap class. The implementation as follows:

public static Bitmap MedianFilter(this Bitmap sourceBitmap, 
                                  int matrixSize) 
{ 
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length]; 
    byte[] middlePixel; 


    int imageStride = sourceBitmap.Width * 4; 
    int filterOffset = (matrixSize - 1) / 2; 
    int calcOffset = 0, filterY = 0, filterX = 0; 
    List<int> neighbourPixels = new List<int>(); 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    { 
        filterY = -filterOffset; filterX = -filterOffset; 
        neighbourPixels.Clear(); 


        while (filterY <= filterOffset) 
        { 
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            if (calcOffset > 0 &&  
                calcOffset + 4 < pixelBuffer.Length) 
            { 
                neighbourPixels.Add(BitConverter.ToInt32( 
                                    pixelBuffer, calcOffset)); 
            } 


            filterX++; 


            if (filterX > filterOffset) 
             { filterX = -filterOffset; filterY++; }
        }


        neighbourPixels.Sort(); 
        middlePixel = BitConverter.GetBytes( 
                      neighbourPixels[filterOffset]); 


        resultBuffer[k] = middlePixel[0]; 
        resultBuffer[k + 1] = middlePixel[1]; 
        resultBuffer[k + 2] = middlePixel[2]; 
        resultBuffer[k + 3] = middlePixel[3]; 
    }


    return resultBuffer.GetImage(sourceBitmap.Width,  
                                 sourceBitmap.Height); 
}

Flower: Distortion Factor 25

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Lilium chalcedonicum in habitat at Hrisomiglia, Greece.
Attribution: Ernst Gügel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Lilium ponticum in habitat near Ikizdere, Turkey.
Attribution: Ernst Gügel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Lilium sargentiae flora.
Attribution: Denis Barthel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

A lilium longiflorum, commonly known as an Easter Lily.
Attribution: Matt H. Wade. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Flora Lilium bulbiferum ssp. croceum, ex coll. Monte Adone, Bologna, Italia.
Attribution: Denis Barthel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Turks Cap Lily the Great Smoky Mountains National Park in western North Carolina.
Attribution: Arx Fortis. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Orange Lily in full bloom showing pollen covered stamens, Ontario, Canada. June 2002.
Attribution: Relic38. This file is licensed under the Creative Commons Attribution 3.0 Unported license.
Download from Wikipedia

Zantedeschia aethiopica (common names calla lily, arum lily).
Attribution: Two+two=4. This file has been released into the public domain. This applies worldwide.
Download from Wikipedia

C# How to: Fuzzy Blur Filter

Published August 9, 2013 Augmented Reality , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Image Processing , Microsoft , Morphology Filters , New Version , Non-Photorealistic Rendering , Opensource , Tip , Update 3 Comments
Tags: Alpha Red Green Blue, Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, Boolean Edge Detection, Box Blur, C#, Calculate Matrix, Calculating Kernels, Code Sample, Color Filters, Computer vision, Converting Images, Convolution filters, Convolution Kernel, Convolution matrix, Edge Detect, Edge Detection, Edge enhance, Edge Masks, Extension Methods, Feature extraction, Fuzzy Blur, Graphic Filters, How to, Image, Image Blur, Image Edge Detection, Image Intensity, Image Manipulation, Image processing, Image Transform, Machine vision, Morphologial Filters, Non-Photorealistic Rendering, Pixel Filters

Article Purpose

This article serves to illustrate the concepts involved in implementing a Fuzzy Blur Filter. This filter results in rendering non-photo realistic images which express a certain artistic effect.

Frog: Filter Size 19×19

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample source code accompanying this article includes a Windows Forms based test application. The concepts explored throughout this article can be replicated/tested using the sample application.

When executing the sample application the user interface exposes a number of configurable options:

Loading and Saving Images – Users are able to load source/input images from the local file system by clicking the Load Image button. Clicking the Save Image button allow users to save filter result images.
Filter Size – The specified filter size affects the filter intensity. Smaller filter sizes result in less blurry images being rendered, whereas larger filter sizes result in more blurry images being rendered.
Edge Factors – The contrast of fuzzy image noise expressed in resulting images depend on the specified edge factor values. Values less than one result in detected image edges being darkened and values greater than one result in detected image edges being lightened.

The following image is a screenshot of the Fuzzy Blur Filter sample application in action:

Frog: Filter Size 9×9

Fuzzy Blur Overview

The Fuzzy Blur Filter relies on the interference of image noise when performing edge detection in order to create a fuzzy effect. In addition image blurring results from performing a mean filter.

The steps involved in performing a Fuzzy Blur Filter can be described as follows:

Edge Detection and Enhancement – Using the first edge factor specified enhance image edges by performing Boolean Edge detection. Being sensitive to image noise, a fair amount of detected image edges will actually be image noise in addition to actual image edges.
Mean Filter Blur – Using the edge enhanced image created in the previous step perform a mean filter blur. The enhanced edges will be blurred since a Mean filter does not have edge preservation properties. The size of the Mean filter implemented depends on a user specified value.
Edge Detection and Enhancement – Using the Mean filter blurred image created in the previous step once again perform Boolean Edge detection, enhancing detected edges according to the second edge factor specified.

Frog: Filter Size 9×9

Mean Filter Blurring

A Mean Filter Blur, also known as a Box Blur, can be performed through image convolution. The size of the matrix/kernel implemented when preforming image convolution will be determined through user input.

Every matrix/kernel element should be set to one. The resulting value should be multiplied by a factor value equating to one divided by the matrix/kernel size. As an example, a matrix/kernel size of 3×3 can be expressed as follows:

An alternative expression can also be:

Frog: Filter Size 9×9

Boolean Edge Detection without a local threshold

When performing Boolean Edge Detection a local threshold should be implemented in order to exclude image noise. In this article we rely on the interference of image noise in order to render a fuzzy image effect. By not implementing a local threshold when performing Boolean Edge detection the sample source code ensures sufficient interference from image noise.

The steps involved in performing Boolean Edge Detection without a local threshold can be described as follows:

Calculate Neighbourhood Mean – Iterate each pixel forming part of the source/input image. Using a 3×3 matrix size calculate the mean value of the neighbourhood surrounding the pixel currently being iterated.
Create Mean comparison Matrix – Once again using a 3×3 matrix size compare each neighbourhood pixel to the newly calculated mean value. Create a temporary 3×3 size matrix, each matrix element’s value should be the result of mean comparison. Should the value expressed by a neighbourhood pixel exceed the mean value the corresponding temporary matrix element should be set to one. When the calculated mean value exceeds the value of a neighbourhood pixel the corresponding temporary matrix element should be set to zero.
Compare Edge Masks – Using sixteen predefined edge masks compare the temporary matrix created in the previous step to each edge mask. If the temporary matrix matches one of the predefined edge masks multiply the specified factor to the pixel currently being iterated.

Note: A detailed article on Boolean Edge detection implementing a local threshold can be found here: C# How to: Boolean Edge Detection

Frog: Filter Size 9×9

The sixteen predefined edge masks each represent an image edge in a different direction. The predefined edge masks can be expressed as:

Frog: Filter Size 13×13

Implementing a Mean Filter

The sample source code defines the MeanFilter method, an extension method targeting the Bitmap class. The definition listed as follows:

private static Bitmap MeanFilter(this Bitmap sourceBitmap, 
                                 int meanSize)
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length];


    double blue = 0.0, green = 0.0, red = 0.0;
    double factor = 1.0 / (meanSize * meanSize);


    int imageStride = sourceBitmap.Width * 4;
    int filterOffset = meanSize / 2; 
    int calcOffset = 0, filterY = 0, filterX = 0; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4)
    {
        blue = 0; green = 0; red = 0;
        filterY = -filterOffset;
        filterX = -filterOffset;


        while (filterY <= filterOffset)
        {
            calcOffset = k + (filterX * 4) +
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 :
            (calcOffset >= pixelBuffer.Length - 2 ?
            pixelBuffer.Length - 3 : calcOffset));


            blue += pixelBuffer[calcOffset];
            green += pixelBuffer[calcOffset + 1];
            red += pixelBuffer[calcOffset + 2];


            filterX++;


            if (filterX > filterOffset)
            {
                filterX = -filterOffset;
                filterY++;
            }
        }


        resultBuffer[k] = ClipByte(factor * blue);
        resultBuffer[k + 1] = ClipByte(factor * green);
        resultBuffer[k + 2] = ClipByte(factor * red);
        resultBuffer[k + 3] = 255;
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height);
}

Frog: Filter Size 19×19

Implementing Boolean Edge Detection

Boolean Edge detection is performed in the sample source code through the implementation of the BooleanEdgeDetectionFilter method. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the BooleanEdgeDetectionFilter extension method:

public static Bitmap BooleanEdgeDetectionFilter( 
       this Bitmap sourceBitmap, float edgeFactor) 
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length]; 
    Buffer.BlockCopy(pixelBuffer, 0, resultBuffer, 
                     0, pixelBuffer.Length); 


    List<string> edgeMasks = GetBooleanEdgeMasks(); 
 
    int imageStride = sourceBitmap.Width * 4; 
    int matrixMean = 0, pixelTotal = 0; 
    int filterY = 0, filterX = 0, calcOffset = 0; 
    string matrixPatern = String.Empty; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    {
        matrixPatern = String.Empty; 
        matrixMean = 0; pixelTotal = 0; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 
 
            matrixMean += pixelBuffer[calcOffset]; 
            matrixMean += pixelBuffer[calcOffset + 1]; 
            matrixMean += pixelBuffer[calcOffset + 2]; 


            filterX += 1; 


            if (filterX > 1) 
             { filterX = -1; filterY += 1; } 
        }


        matrixMean = matrixMean / 9; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 


            pixelTotal = pixelBuffer[calcOffset]; 
            pixelTotal += pixelBuffer[calcOffset + 1]; 
            pixelTotal += pixelBuffer[calcOffset + 2]; 
 
            matrixPatern += (pixelTotal > matrixMean 
                                       ? "1" : "0"); 
            filterX += 1; 


            if (filterX > 1) 
            { filterX = -1; filterY += 1; } 
        } 


        if (edgeMasks.Contains(matrixPatern)) 
        {
            resultBuffer[k] = 
            ClipByte(resultBuffer[k] * edgeFactor); 


            resultBuffer[k + 1] = 
            ClipByte(resultBuffer[k + 1] * edgeFactor); 


            resultBuffer[k + 2] = 
            ClipByte(resultBuffer[k + 2] * edgeFactor); 
        }
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height); 
}

Frog: Filter Size 13×13

The predefined edge masks implemented in mean comparison have been wrapped by the GetBooleanEdgeMasks method. The definition as follows:

public static List<string> GetBooleanEdgeMasks() 
{
    List<string> edgeMasks = new List<string>(); 


    edgeMasks.Add("011011011"); 
    edgeMasks.Add("000111111"); 
    edgeMasks.Add("110110110"); 
    edgeMasks.Add("111111000"); 
    edgeMasks.Add("011011001"); 
    edgeMasks.Add("100110110"); 
    edgeMasks.Add("111011000"); 
    edgeMasks.Add("111110000"); 
    edgeMasks.Add("111011001"); 
    edgeMasks.Add("100110111"); 
    edgeMasks.Add("001011111"); 
    edgeMasks.Add("111110100"); 
    edgeMasks.Add("000011111"); 
    edgeMasks.Add("000110111"); 
    edgeMasks.Add("001011011"); 
    edgeMasks.Add("110110100"); 


    return edgeMasks; 
}

Frog: Filter Size 19×19

Implementing a Fuzzy Blur Filter

The FuzzyEdgeBlurFilter method serves as the implementation of a Fuzzy Blur Filter. As discussed earlier a Fuzzy Blur Filter involves enhancing image edges through Boolean Edge detection, performing a Mean Filter blur and then once again performing Boolean Edge detection. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the FuzzyEdgeBlurFilter method:

public static Bitmap FuzzyEdgeBlurFilter(this Bitmap sourceBitmap,  
                                         int filterSize,  
                                         float edgeFactor1,  
                                         float edgeFactor2) 
{
    return  
    sourceBitmap.BooleanEdgeDetectionFilter(edgeFactor1). 
    MeanFilter(filterSize).BooleanEdgeDetectionFilter(edgeFactor2); 
}

Frog: Filter Size 3×3

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Tyler’s Tree Frog
Attribution: LiquidGhoul. This file has been released into the public domain by its author, LiquidGhoul. This applies worldwide.
Download from Wikipedia.

Phyllobates Terribilis
Attribution: Wilfried Berns. This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Germany license.
Download from Wikipedia.

Dendropsophus Microcephalus
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia

Panamanian Golden Frog
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia.

C# How to: Image Convolution

Published May 1, 2013 Augmented Reality , C# , Code Samples , Extension Methods , Generics , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , Opensource , Wikipedia 31 Comments
Tags: Alpha Red Green Blue, Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, C#, C# Convolution, Code Sample, Convolution filters, Convolution Kernel, Convolution matrix, Edge Detect, Emboss, Gaussian Blur, Graphic Filters, High pass, Image Manipulation, Image Noise, Image Transform, Matrix, Motion Blur, Pixel Filters, Pixel Manipulation, Sharpen

Article Purpose

This article is intended to serve as an introduction to the concepts related to creating and processing convolution filters being applied on images. The Convolution filters discussed are: Blur, Gaussian Blur, Soften, Motion Blur, High Pass, Edge Detect, Sharpen and Emboss.

Sample Source code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

A Sample Application has been included with this article’s sample source code. The Sample Application has been developed to target the Windows Forms platform. Using the Sample Application users are able to select a source/input image from the local file system and from a drop down ComboBox select a Convolution filter to apply. Filtered images can be saved to the local file system when a user clicks the ‘Save’ button.

The following screenshot shows the Image Convolution Filter sample application in action.

Image Convolution

Before delving into discussions on technical implementation details it is important to have a good understanding of the concepts behind Image Convolution.

In relation to image processing Convolution can be considered as algorithms being implemented resulting in translating input/source images. Algorithms being applied generally take the form of accepting two input values and producing a third value considered to be a modified version of one of the input values.

Image Convolution can be implemented to produce image filters such as: Blurring, Smoothing, Edge Detection, Sharpening and Embossing. The resulting filtered images still bares a relation to the input source image.

Convolution Matrix

In this article we will be implementing Convolution through means of a matrix or kernel representing the algorithms required to produce resulting filtered images. A Matrix should be considered as a two dimensional array or grid. It is required that the number or rows and columns be of an equal size, which is furthermore required to not be a factor of two. Examples of valid matrix dimensions could be 3×3 or 5×5. Dimensions such as 2×2 or 4×4 would not be valid. Generally the sum total of all the values expressed in a matrix equates to one, although it is not a strict requirement.

The following table represents an example matrix/kernel:

2	0	0
0	-1	0
0	0	-1

An important aspect to keep in mind: When implementing a convolution matrix the value of a pixel will be determined by the values of the pixel’s neighbouring pixels. The values contained in a matrix represent factor values intended to be multiplied with pixel values. In a convolution matrix the centre pixel represents the pixel currently being modified. Neighbouring matrix values express the factor to be applied to the corresponding neighbouring pixels in regards to the pixel currently being modified.

The ConvolutionFilterBase class

The sample code defines the abstract class ConvolutionFilterBase. This class is intended to represent the minimum requirements of a convolution matrix. When defining a convolution matrix we will be inheriting from the ConvolutionFilterBase class. Because this class and its members have been defined as abstract, implementing classes are required to implement all defined abstract members.

The following code snippet details the ConvolutionFilterBase definition:

public abstract class ConvolutionFilterBase 
{ 
    public abstract string FilterName 
    {
        get; 
    }

           
    public abstract double Factor 
    {
        get; 
    } 

   
    public abstract double Bias 
    { 
        get; 
    } 

   
    public abstract double[,] FilterMatrix 
    {
        get; 
    } 
}

As to be expected the member property FilterMatrix is intended to represent a two dimensional array containing a convolution matrix. In some instances when the sum total of matrix values do not equate to 1 a filter might implement a Factor value other than the default of 1. Additionally some filters may also require a Bias value to be added the final result value when calculating the matrix.

Calculating a Convolution Filter

Calculating convolution filters and creating the resulting Bitmap images can be achieved by invoking the ConvolutionFilter method. This method is defined as an extension method targeting the Bitmap class. The definition of the ConvolutionFilter extension method as follows:

 public static Bitmap ConvolutionFilter<T>(this Bitmap sourceBitmap, T filter)  
                                 where T : ConvolutionFilterBase 
{ 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0, 
                                sourceBitmap.Width, sourceBitmap.Height), 
                                ImageLockMode.ReadOnly, PixelFormat.Format32bppArgb); 

  
    byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

    
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 

    
    sourceBitmap.UnlockBits(sourceData); 

    
    double blue = 0.0; 
    double green = 0.0; 
    double red = 0.0; 

    
    int filterWidth = filter.FilterMatrix.GetLength(1); 
    int filterHeight = filter.FilterMatrix.GetLength(0); 

    
    int filterOffset = (filterWidth-1) / 2; 
    int calcOffset = 0; 

    
    int byteOffset = 0; 

    
    for (int offsetY = filterOffset; offsetY <  
         sourceBitmap.Height - filterOffset; offsetY++) 
    { 
        for (int offsetX = filterOffset; offsetX <  
             sourceBitmap.Width - filterOffset; offsetX++) 
        { 
            blue = 0; 
            green = 0; 
            red = 0; 

    
            byteOffset = offsetY *  
                            sourceData.Stride +  
                            offsetX * 4; 

    
            for (int filterY = -filterOffset;  
                 filterY <= filterOffset; filterY++) 
            {
                for (int filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                { 

    
                    calcOffset = byteOffset +  
                                 (filterX * 4) +  
                                 (filterY * sourceData.Stride); 

    
                    blue += (double)(pixelBuffer[calcOffset]) *  
                             filter.FilterMatrix[filterY + filterOffset,  
                             filterX + filterOffset]; 

    
                    green += (double)(pixelBuffer[calcOffset + 1]) *  
                              filter.FilterMatrix[filterY + filterOffset,  
                              filterX + filterOffset]; 

    
                    red += (double)(pixelBuffer[calcOffset + 2]) *  
                            filter.FilterMatrix[filterY + filterOffset,  
                            filterX + filterOffset]; 
                } 
            }

    
            blue = filter.Factor * blue + filter.Bias; 
            green = filter.Factor * green + filter.Bias; 
            red = filter.Factor * red + filter.Bias; 

    
            if (blue > 255) 
            { blue = 255; } 
             else if (blue < 0) 
            { blue = 0; } 

    
            if (green > 255) 
            { green = 255; } 
             else if (green < 0) 
            { green = 0; } 

    
            if (red > 255) 
            { red = 255; } 
             else if (red < 0) 
            { red = 0; } 

    
            resultBuffer[byteOffset] = (byte)(blue); 
            resultBuffer[byteOffset + 1] = (byte)(green); 
            resultBuffer[byteOffset + 2] = (byte)(red); 
            resultBuffer[byteOffset + 3] = 255; 
        } 
    } 

    
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 

    
    BitmapData resultData = resultBitmap.LockBits(new Rectangle(0, 0, 
                            resultBitmap.Width, resultBitmap.Height), 
                            ImageLockMode.WriteOnly, PixelFormat.Format32bppArgb); 

    
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

    
    return resultBitmap; 
}

The following section provides a detailed discussion of the ConvolutionFilter extension method.

ConvolutionFilter<T> – Method Signature

public static Bitmap ConvolutionFilter<T>
                     (this Bitmap sourceBitmap,
                      T filter)  
                      where T : ConvolutionFilterBase

The ConvolutionFilter method defines a generic type T constrained by the requirement to be of type ConvolutionFilterBase. The filter parameter being of generic type T has to be of type ConvolutionFilterBase or a type which inherits from the ConvolutionFilterBase class.

Notice how the sourceBitmap parameter type definition is preceded by the this keyword indicating the method can be implemented as an extension method. Keep in mind extension methods are required to be declared as static.

The sourceBitmap parameter represents the source/input Bitmap upon which the filter is to be applied. Note that the ConvolutionFilter method is implemented as immutable. The input parameter values are not modified, instead a new Bitmap instance will be created and returned.

ConvolutionFilter<T> – Creating the Data Buffer

BitmapData sourceData = sourceBitmap.LockBits
                             (new Rectangle(0, 0,
                             sourceBitmap.Width, 
                             sourceBitmap.Height),
                             ImageLockMode.ReadOnly,
                             PixelFormat.Format32bppArgb);

  
byte[] pixelBuffer = new byte[sourceData.Stride *
                              sourceData.Height];

  
byte[] resultBuffer = new byte[sourceData.Stride *
                               sourceData.Height]; 

    
Marshal.Copy(sourceData.Scan0, pixelBuffer,
             0, pixelBuffer.Length);

    
sourceBitmap.UnlockBits(sourceData);

In order to access the underlying ARGB values from a Bitmap object we first need to lock the Bitmap into memory by invoking the Bitmap.LockBits method. Locking a Bitmap into memory prevents the Garbage Collector from moving a Bitmap object to a new location in memory.

When invoking the Bitmap.LockBits method the source code instantiates a BitmapData object from the return value. The BitmapData.Stride property represents the number of bytes in a single Bitmap pixel row. In this scenario the BitmapData.Stride property should be equal to the Bitmap’s width in pixels multiplied by four seeing as every pixel consists of four bytes: Alpha, Red, Green and Blue.

The ConvolutionFilter method defines two byte buffers, of which the size is set to equal the size of the Bitmap’s underlying data. The BitmapData property BitmapData.Scan0 of type IntPtr represents the memory address of the first byte value of a Bitmap’s underlying byte buffer. Using the Marshal.Copy method we specify the starting point memory address from where to start copying the Bitmap’s byte buffer.

Important to remember is the next operation being performed: invoking the Bitmap.UnlockBits method. If a Bitmap has been locked into memory ensure releasing the lock by invoking the Bitmap.UnlockBits method.

ConvolutionFilter<T> – Iterating Rows and Columns

double blue = 0.0; 
double green = 0.0; 
double red = 0.0; 

    
int filterWidth = filter.FilterMatrix.GetLength(1); 
int filterHeight = filter.FilterMatrix.GetLength(0); 

    
int filterOffset = (filterWidth-1) / 2; 
int calcOffset = 0; 

    
int byteOffset = 0; 

    
for (int offsetY = filterOffset; offsetY <  
     sourceBitmap.Height - filterOffset; offsetY++) 
{ 
    for (int offsetX = filterOffset; offsetX <  
         sourceBitmap.Width - filterOffset; offsetX++) 
    { 
         blue = 0; 
         green = 0; 
         red = 0; 

    
         byteOffset = offsetY *  
                      sourceData.Stride +  
                      offsetX * 4;

The ConvolutionFilter method employs two for loops in order to iterate each pixel represented in the ARGB data buffer. Defining two for loops to iterate a one dimensional array simplifies the concept of accessing the array in terms of rows and columns.

Note that the inner loop is limited to the width of the source/input Bitmap parameter, in other words the number of horizontal pixels. Remember that the data buffer represents four bytes, Alpha, Red, Green and Blue, for each pixel. The inner loop therefore iterates entire pixels.

As discussed earlier the filter matrix has to be declared as a two dimensional array with the same odd number of rows and columns. If the current pixel being processed relates to the element at the centre of the matrix, the width of the matrix less one divided by two equates to the neighbouring pixel index values.

The index of the current pixel can be calculated by multiplying the current row index (offsetY) and the number of ARGB byte values per row of pixels (sourceData.Stride), to which is added the current column/pixel index (offsetX) multiplied by four.

ConvolutionFilter<T> – Iterating the Matrix

for (int filterY = -filterOffset;  
     filterY <= filterOffset; filterY++) 
{
    for (int filterX = -filterOffset; 
         filterX <= filterOffset; filterX++) 
    { 
        calcOffset = byteOffset +  
                     (filterX * 4) +  
                     (filterY * sourceData.Stride); 

    
        blue += (double)(pixelBuffer[calcOffset]) *  
                 filter.FilterMatrix[filterY + filterOffset,  
                 filterX + filterOffset]; 

    
        green += (double)(pixelBuffer[calcOffset + 1]) *  
                  filter.FilterMatrix[filterY + filterOffset,  
                  filterX + filterOffset]; 

    
        red += (double)(pixelBuffer[calcOffset + 2]) *  
                filter.FilterMatrix[filterY + filterOffset,  
                filterX + filterOffset]; 
    } 
}

The ConvolutionFilter method iterates the two dimensional matrix by implementing two for loops, iterating rows and for each row iterating columns. Both loops have been declared to have a starting point equal to the negative value of half the matrix length (filterOffset). Initiating the loops with negative values simplifies implementing the concept of neighbouring pixels.

The first statement performed within the inner loop calculates the index of the neighbouring pixel in relation to the current pixel. Next the matrix value is applied as a factor to the corresponding neighbouring pixel’s individual colour components. The results are added to the totals variables blue, green and red.

In regards to each iteration iterating in terms of an entire pixel, to access individual colour components the source code adds the required colour component offset. Note: ARGB colour components are in fact expressed in reversed order: Blue, Green, Red and Alpha. In other words, a pixel’s first byte (offset 0) represents Blue, the second (offset 1) represents Green, the third (offset 2) represents Red and the last (offset 3) representing the Alpha component.

ConvolutionFilter<T> – Applying the Factor and Bias

blue = filter.Factor * blue + filter.Bias; 
green = filter.Factor * green + filter.Bias; 
red = filter.Factor * red + filter.Bias; 

    
if (blue > 255) 
{ blue = 255; } 
 else if (blue < 0) 
{ blue = 0; } 

    
if (green > 255) 
{ green = 255; } 
 else if (green < 0) 
{ green = 0; } 

    
if (red > 255) 
{ red = 255; } 
 else if (red < 0) 
{ red = 0; } 

    
resultBuffer[byteOffset] = (byte)(blue); 
resultBuffer[byteOffset + 1] = (byte)(green); 
resultBuffer[byteOffset + 2] = (byte)(red); 
resultBuffer[byteOffset + 3] = 255;

After iterating the matrix and calculating the matrix values of the current pixel’s Red, Green and Blue colour components we apply the Factor and add the Bias defined by the filter parameter.

Colour components may only contain a value ranging from 0 to 255 inclusive. Before we assign the newly calculated colour component value we ensure that the value falls within the required range. Values which exceed 255 are set to 255 and values less than 0 are set to 0. Note that assignment is implemented in terms of the result buffer, the original source image buffer remains unchanged.

ConvolutionFilter<T> – Returning the Result

Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, 
                                 sourceBitmap.Height); 

    
BitmapData resultData = resultBitmap.LockBits(
                        new Rectangle(0, 0, 
                        resultBitmap.Width,
                        resultBitmap.Height), 
                        ImageLockMode.WriteOnly,
                        PixelFormat.Format32bppArgb); 

    
Marshal.Copy(resultBuffer, 0, resultData.Scan0, 
                              resultBuffer.Length);

  
resultBitmap.UnlockBits(resultData); 

    
return resultBitmap;

The final steps performed by the ConvolutionFilter method involves creating a new Bitmap object instance and copying the calculated result buffer. In a similar fashion to reading underlying pixel data we copy the result buffer to the Bitmap object.

Creating Filters

The main requirement when creating a filter is to inherit from the abstract ConvolutionBaseFilter class. The following sections of this article will discuss various filter types and variations where applicable.

To illustrate the different effects resulting from applying filters all of the filters discussed make use of the same source image. The original image file is licensed under the Creative Commons Attribution 2.0 Generic license and can be downloaded from:

http://commons.wikimedia.org/wiki/File:Ara_macao_-on_a_small_bicycle-8.jpg

Blur Filters

Image blurring is typically used to reduce image noise and detail. The filter’s matrix size affects the level of blurring. A larger matrix results in higher level of blurring, whereas a smaller matrix results in a lesser level of blurring.

Blur3x3Filter

The Blur3x3Filter results in a slight to medium level of image blurring. The matrix consists of 9 elements in a 3×3 configuration.

public class Blur3x3Filter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Blur3x3Filter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 0.0, 0.2, 0.0, },  
                        { 0.2, 0.2, 0.2, },  
                        { 0.0, 0.2, 0.2, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Blur5x5Filter

The Blur5x5Filter results in a medium level of image blurring. The matrix consists of 25 elements in a 5×5 configuration. Notice the factor of 1.0 / 13.0.

public class Blur5x5Filter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Blur5x5Filter"; } 
    }

   
    private double factor = 1.0 / 13.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 0, 0, 1, 0, 0, }, 
                        { 0, 1, 1, 1, 0, }, 
                        { 1, 1, 1, 1, 1, }, 
                        { 0, 1, 1, 1, 0, }, 
                        { 0, 0, 1, 0, 0, }, };  

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Gaussian3x3BlurFilter

The Gaussian3x3BlurFilter implements a Gaussian blur through a matrix of 9 elements in a 3×3 configuration. The sum total of all matrix elements equal 16, therefore the Factor is defined as 1.0 / 16.0. Applying this filter results in a slight to medium level of blurring.

public class Gaussian3x3BlurFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Gaussian3x3BlurFilter"; } 
    }

   
    private double factor = 1.0 / 16.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 1, 2, 1, },  
                        { 2, 4, 2, },  
                        { 1, 2, 1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Gaussian5x5BlurFilter

The Gaussian5x5BlurFilter implements a Gaussian blur through a matrix of 25 elements in a 5×5 configuration. The sum total of all matrix elements equal 159, therefore the Factor is defined as 1.0 / 159.0. Applying this filter results in a medium level of blurring.

public class Gaussian5x5BlurFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Gaussian5x5BlurFilter"; } 
    }

   
    private double factor = 1.0 / 159.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 2, 04, 05, 04, 2, }, 
                        { 4, 09, 12, 09, 4, }, 
                        { 5, 12, 15, 12, 5, }, 
                        { 4, 09, 12, 09, 4, }, 
                        { 2, 04, 05, 04, 2, }, };  

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

MotionBlurFilter

By implementing the MotionBlurFilter resulting images indicate the appearance of a high level of blurring associated with motion/movement. This filter is a combination of left to right and right to left motion blurring. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "MotionBlurFilter"; } 
    }

   
    private double factor = 1.0 / 18.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                        { 0, 1, 0, 0, 0, 0, 0, 1, 0, },
                        { 0, 0, 1, 0, 0, 0, 1, 0, 0, },
                        { 0, 0, 0, 1, 0, 1, 0, 0, 0, },
                        { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                        { 0, 0, 0, 1, 0, 1, 0, 0, 0, },
                        { 0, 0, 1, 0, 0, 0, 1, 0, 0, },
                        { 0, 1, 0, 0, 0, 0, 0, 1, 0, },
                        { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

MotionBlurLeftToRightFilter

The MotionBlurLeftToRightFilter creates the effect of blurring as a result of left to right movement. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurLeftToRightFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "MotionBlurLeftToRightFilter"; } 
    }

   
    private double factor = 1.0 / 9.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, 
                        { 0, 1, 0, 0, 0, 0, 0, 0, 0, },
                        { 0, 0, 1, 0, 0, 0, 0, 0, 0, },
                        { 0, 0, 0, 1, 0, 0, 0, 0, 0, },
                        { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                        { 0, 0, 0, 0, 0, 1, 0, 0, 0, },
                        { 0, 0, 0, 0, 0, 0, 1, 0, 0, },
                        { 0, 0, 0, 0, 0, 0, 0, 1, 0, },
                        { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

MotionBlurRightToLeftFilter

The MotionBlurRightToLeftFilter creates the effect of blurring as a result of right to left movement. The matrix consists of 81 elements in a 9×9 configuration.

public class MotionBlurRightToLeftFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "MotionBlurRightToLeftFilter"; } 
    }

   
    private double factor = 1.0 / 9.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                        { 0, 0, 0, 0, 0, 0, 0, 1, 0, },
                        { 0, 0, 0, 0, 0, 0, 1, 0, 0, },
                        { 0, 0, 0, 0, 0, 1, 0, 0, 0, },
                        { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                        { 0, 0, 0, 1, 0, 0, 0, 0, 0, },
                        { 0, 0, 1, 0, 0, 0, 0, 0, 0, },
                        { 0, 1, 0, 0, 0, 0, 0, 0, 0, },
                        { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Soften Filter

The SoftenFilter can be used to smooth or soften an image. The matrix consists of 9 elements in a 3×3 configuration.

public class SoftenFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "SoftenFilter"; } 
    }

   
    private double factor = 1.0 / 8.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 1, 1, 1, },  
                        { 1, 1, 1, },  
                        { 1, 1, 1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Sharpen Filters

Sharpening an image does not add additional detail to an image but rather adds emphasis to existing image details. Image sharpness is sometimes referred to as image crispness.

SharpenFilter

This filter is intended as a general usage sharpen filter. In a variety of scenarios this filter should provide a reasonable level of image sharpening depending on source image quality.

public class SharpenFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "SharpenFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -1, -1, },  
                        { -1,  9, -1, },  
                        { -1, -1, -1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Sharpen3x3Filter

The Sharpen3x3Filter results in a medium level of image sharpness, less intense when compared to the SharpenFilter discussed previously.

public class Sharpen3x3Filter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Sharpen3x3Filter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { {  0, -1,  0, },  
                        { -1,  5, -1, },  
                        {  0, -1,  0, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Sharpen3x3FactorFilter

The Sharpen3x3FactorFilter provides a level of image sharpness similar to the Sharpen3x3Filter explored previously. Both filters define a 9 element 3×3 matrix. The filters differ in regards to Factor values. The Sharpen3x3Filter matrix values equate to a sum total of 1, the Sharpen3x3FactorFilter in contrast equate to a sum total of 3. The Sharpen3x3FactorFilter defines a Factor of 1 / 3, resulting in matrix sum total being negated to 1.

public class Sharpen3x3FactorFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Sharpen3x3FactorFilter"; } 
    }

   
    private double factor = 1.0 / 3.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { {  0, -2,  0, },  
                        { -2, 11, -2, },  
                        {  0, -2,  0, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Sharpen5x5Filter

The Sharpen5x5Filter matrix defines 25 elements in a 5×5 configuration. The level of image sharpness resulting from implementing this filter to a greater extent is depended on the source image. In some scenarios result images may appear slightly softened.

public class Sharpen5x5Filter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Sharpen5x5Filter"; } 
    }

   
    private double factor = 1.0 / 8.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -1, -1, -1, -1, }, 
                        { -1,  2,  2,  2, -1, },
                        { -1,  2,  8,  2,  1, },
                        { -1,  2,  2,  2, -1, },
                        { -1, -1, -1, -1, -1, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

IntenseSharpenFilter

The IntenseSharpenFilter produces result images with overly emphasized edge lines.

public class IntenseSharpenFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "IntenseSharpenFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 1,  1, 1, },  
                        { 1, -7, 1, },  
                        { 1,  1, 1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Edge Detection Filters

Edge detection is the first step towards feature detection and feature extraction in digital image processing. Edges are generally perceived in images in areas exhibiting sudden differences in brightness.

EdgeDetectionFilter

The EdgeDetectionFilter is intended to be used as a general purpose edge detection filter, considered appropriate in the majority of scenarios applied.

public class EdgeDetectionFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "EdgeDetectionFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -1, -1, },  
                        { -1,  8, -1, },  
                        { -1, -1, -1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

EdgeDetection45DegreeFilter

The EdgeDetection45DegreeFilter has the ability to detect edges at 45 degree angles more effectively than other edge detection filters.

public class EdgeDetection45DegreeFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "EdgeDetection45DegreeFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1,  0,  0,  0,  0, }, 
                        {  0, -2,  0,  0,  0, },
                        {  0,  0,  6,  0,  0, },
                        {  0,  0,  0, -2,  0, },
                        {  0,  0,  0,  0, -1, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

HorizontalEdgeDetectionFilter

The HorizontalEdgeDetectionFilter has the ability to detect horizontal edges more effectively than other edge detection filters.

public class HorizontalEdgeDetectionFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "HorizontalEdgeDetectionFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { {  0,  0,  0,  0,  0, }, 
                        {  0,  0,  0,  0,  0, },
                        { -1, -1,  2,  0,  0, },
                        {  0,  0,  0,  0,  0, },
                        {  0,  0,  0,  0,  0, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

VerticalEdgeDetectionFilter

The VerticalEdgeDetectionFilter has the ability to detect vertical edges more effectively than other edge detection filters.

public class VerticalEdgeDetectionFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "VerticalEdgeDetectionFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 0,  0, -1,  0,  0, }, 
                        { 0,  0, -1,  0,  0, },
                        { 0,  0,  4,  0,  0, },
                        { 0,  0, -1,  0,  0, },
                        { 0,  0, -1,  0,  0, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

EdgeDetectionTopLeftBottomRightFilter

This filter closely resembles an embossed image indicating object depth whilst still providing a reasonable level of edge detection detail.

public class EdgeDetectionTopLeftBottomRightFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "EdgeDetectionTopLeftBottomRightFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 0.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -5,  0,  0, },  
                        {  0,  0,  0, },  
                        {  0,  0,  5, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Emboss Filters

Emboss filters produce result images with an emphasis on depth, based on lines/edges expressed in an input/source image. Result images give the impression of being three dimensional to a varying extent, depended on image details defined by input images.

EmbossFilter

The EmbossFilter is intended as a general application emboss filter. Take note of the Bias value of 128. Without a bias value, result images would be very dark or mostly black.

public class EmbossFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "EmbossFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 128.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { 2,  0,  0, },  
                        { 0, -1,  0, },  
                        { 0,  0, -1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Emboss45DegreeFilter

The Emboss45DegreeFilter has the ability to produce result images with good emphasis on 45 degree edges/lines.

public class Emboss45DegreeFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "Emboss45DegreeFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 128.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -1,  0, },  
                        { -1,  0,  1, },  
                        {  0,  1,  1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

EmbossTopLeftBottomRightFilter

The EmbossTopLeftBottomRightFilter provides a more subtle level of embossed result images.

public class EmbossTopLeftBottomRightFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "EmbossTopLeftBottomRightFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 128.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, 0, 0, },  
                        {  0, 0, 0, },  
                        {  0, 0, 1, }, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

IntenseEmbossFilter

When implementing the IntenseEmbossFilter result images provide a good three dimensional/depth level. A drawback of this filter can sometimes be noticed in a reduction image detail.

public class IntenseEmbossFilter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "IntenseEmbossFilter"; } 
    }

   
    private double factor = 1.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 128.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -1, -1, -1,  0, }, 
                        { -1, -1, -1,  0,  1, },
                        { -1, -1,  0,  1,  1, },
                        { -1,  0,  1,  1,  1, },
                        {  0,  1,  1,  1,  1, }, };

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

High Pass

High pass filters produce result images where only high frequency components are retained.

public class HighPass3x3Filter : ConvolutionFilterBase 
{
    public override string FilterName 
    {
        get { return "HighPass3x3Filter"; } 
    }

   
    private double factor = 1.0 / 16.0; 
    public override double Factor 
    { 
        get { return factor; } 
    }

   
    private double bias = 128.0; 
    public override double Bias 
    { 
        get { return bias; }
    } 

   
    private double[,] filterMatrix = 
        new double[,] { { -1, -2, -1, },  
                        { -2, 12, -2, },  
                        { -1, -2, -1,, }; 

   
    public override double[,] FilterMatrix 
    { 
        get { return filterMatrix; } 
    }
}

Posts Tagged 'Blur'

Article Purpose

Sample Source Code

Using the Sample Application

Min/Max Edge Detection

Pixel Neighbourhood

Median Filter

Min/Max Edge Detection Algorithm

Implementing a Min/Max Edge Detection Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Standard Deviation Edge Detection

Pixel Neighbourhood

Pixel Neighbourhood Mean value

Standard Deviation

Standard Deviation Edge Detection Algorithm

Implementing a Standard Deviation Edge Detection filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Image Distortion

Median Filter

Implementing Image Distortion

Implementing a Median Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Fuzzy Blur Overview

Mean Filter Blurring

Boolean Edge Detection without a local threshold

Implementing a Mean Filter

Implementing Boolean Edge Detection

Implementing a Fuzzy Blur Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source code

Using the Sample Application

Image Convolution

Convolution Matrix

The ConvolutionFilterBase class

Calculating a Convolution Filter

ConvolutionFilter<T> – Method Signature

ConvolutionFilter<T> – Creating the Data Buffer

ConvolutionFilter<T> – Iterating Rows and Columns

ConvolutionFilter<T> – Iterating the Matrix

ConvolutionFilter<T> – Applying the Factor and Bias

ConvolutionFilter<T> – Returning the Result

Creating Filters

Blur Filters

Blur3x3Filter

Blur5x5Filter

Gaussian3x3BlurFilter

Gaussian5x5BlurFilter

MotionBlurFilter

MotionBlurLeftToRightFilter

MotionBlurRightToLeftFilter

Soften Filter

Sharpen Filters

SharpenFilter

Sharpen3x3Filter

Sharpen3x3FactorFilter

Sharpen5x5Filter

IntenseSharpenFilter

Edge Detection Filters