Median Filter

Posts Tagged 'Median Filter'

C# How to: Min/Max Edge Detection

Article Purpose

This article serves as a detailed discussion on implementing image edge detection through pixel neighbourhood maximum and minimum value subtraction. Additional concepts illustrated in this article include implementing a median filter and RGB grayscale conversion.

Frog Filter 3×3 Smoothed

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article’s accompanying sample source code includes a Windows Forms based sample application. The sample application provides an implementation of the concepts explored by this article. Concepts discussed can be easily replicated and tested by using the sample application.

Source/input image files can be specified from the local file system when clicking the Load Image button. Additionally users also have the option to save resulting filtered images by clicking the Save Image button.

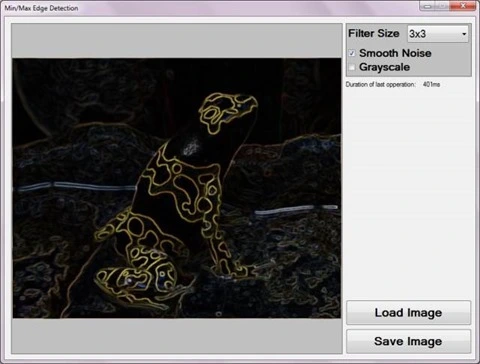
The sample application user interface enables the user to specify three filter configuration values. These values serve as input parameters to the Min/Max Edge Detection Filter and can be described as follows:

Filter Size – Determines the number of surrounding pixels to consider when calculating the minimum and maximum pixel values. This value equates to the size of a pixel’s neighbourhood of pixels. When gradient edges expressed in a source image requires a higher or lower level of expression in result images the filter size value should be adjusted. Higher Filter Size values result in gradient edges being expressed at greater intensity levels in resulting images. Inversely, lower Filter Size values delivers the opposite result of gradient edges being expressed at lesser intensity levels.
Smooth Noise – Image noise when present in source images, can to varying degrees affect the Min/Max Edge Detection Filter’s accuracy in calculating gradient edges. In order to reduce the negative affects of source image noise an image smoothing filter may be implemented. Smoothing out image noise requires additional filter processing and therefore requires additional computation time. If source images reflect minor or no image noise, additional image smoothing may be excluded to reduce filter processing duration.
Grayscale – When required, result images can be expressed in grayscale through configuring this value.

The following image represents a screenshot of the Min/Max Edge Detection Sample application in action.

Min/Max Edge Detection

The method of edge detection illustrated in this article can be classified as a variation of commonly implemented edge detection methods. Image edges expressed within a source image can be determined through the presence of sudden and significant changes in gradient levels that occur within a small/limited perimeter.

As a means to determine gradient level changes the Min/Max Edge Detection algorithm performs pixel neighbourhood inspection, comparing maximum and minimum colour channel values. Should the difference between maximum and minimum colour values be significant, it would be an indication of a significant change in gradient level within the pixel neighbourhood being inspected.

Image noise represents interference in relation to regular gradient level expression. Image noise does not signal the presence of an image edge, although could potentially result in incorrectly determining image edge presence. Image noise and the negative impact thereof can be significantly reduced when applying image smoothing, also sometimes referred to as image blur. The Min/Max Edge Detection algorithm makes provision for optional image smoothing implemented in the form of a median filter.

The following sections provide more detail regarding the concepts introduced in this section, pixel neighbourhood and median filter.

Frog Filter 3×3 Smoothed

Pixel Neighbourhood

A pixel neighbourhood refers to a set of pixels, all of which are related through pixel location coordinates. The width and height of a pixel neighbourhood must be equal, in other words, a pixel neighbourhood can only be square. Additionally, the width/height of a pixel neighbourhood must be an uneven value. When inspecting a pixel’s neighbouring pixels, the pixel being inspected will always be located at the exact center of the pixel neighbourhood. Only when a pixel neighbourhood’s width/height are an uneven value can such a pixel neighbourhood have an exact center pixel. Each pixel represented in an image has a different set of neighbours, some neighbours overlap, but no two pixels have the exact same neighbours. A pixel’s neighbouring pixels can be determined when considering the pixel to be at the center of a block of pixels, extending half the neighbourhood size less one in horizontal, vertical and diagonal directions.

In context of this article and the Min/Max Edge Detection filter, median filtering has been implemented as a means to reduce source image noise. From the Median Wikipedia page we gain the following quote:

In statistics and probability theory, the median is the number separating the higher half of a data sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one (e.g., the median of {3, 3, 5, 9, 11} is 5).

Frog Filter 3×3 Smoothed

The application of a median filter is based in the concept of pixel neighbourhood as discussed earlier. The implementation steps required when applying a median filter can be described as follows:

Iterate every pixel. The pixel neighbourhood of each pixel in a source image needs to be determined and inspected.
Order/Sort pixel neighbourhood values. Once a pixel neighbourhood for a specific pixel has been determined the values expressed by all the pixels in that neighbourhood needs to be sorted or ordered according to value.
Determine midpoint value. In relation to the sorted pixel neighbourhood values, the value positioned exactly halfway between first and last value needs to be determined. As an example, if a pixel neighbourhood contains a total of nine pixels, the midpoint would be at position number five, which is four positions from the first and last value inclusive. The midpoint value in a sorted range of neighbourhood pixel values, is the median value of that pixel neighbourhood’s values.

The median filter should not be confused with the mean filter. A median will always be a midpoint value from a sorted value range, whereas a mean value is equal to the calculated average of a value range. The median filter has the characteristic of reducing image noise whilst still preserving image edges. The mean filter will also reduce image noise, but will do so through generalized image blurring, also referred to as box blur, which does not preserve image edges.

Note that when applying a median filter to RGB colour images median values need to be determined per individual colour channel.

Frog Filter 3×3 Smoothed

Min/Max Edge Detection Algorithm

Image edge detection based in a min/max approach requires relatively few steps, which can be combined in source code implementations to be more efficient from a computational/processing perspective. A higher level logical definition of the steps required can be described as follows:

Image Noise Reduction – If image noise reduction is required apply a median filter to the source image.
Iterate through all of the pixels contained within an image.
For each pixel being iterated, determine the neighbouring pixels. The pixel neighbourhood size will be determined by the specified filter size.
Determine the Minimum and Maximum pixel value expressed within the pixel neighbourhood.
Subtract the Minimum from the Maximum value and assign the result to the pixel currently being iterated.
Apply Grayscale conversion to the pixel currently being iterated, only if grayscale conversion had been configured.

Implementing a Min/Max Edge Detection Filter

The source code implementation of the Min/Max Edge Detection Filter declares two methods, a median filter method and an edge detection method. A median filter and edge detection filter cannot be processed simultaneously. When applying a median filter, the median value of a pixel neighbourhood determined from a source image should be expressed in a separate result image. The original source image should not be altered whilst inspecting pixel neighbourhoods and calculating median values. Only once all pixel values in the result image has been set, can the result image serve as a source image to an edge detection filter method.

The following code snippet provides the source code definition of the MedianFilter method.

private static byte[] MedianFilter(this byte[] pixelBuffer,
                                    int imageWidth,
                                    int imageHeight,
                                    int filterSize)
{
    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;

    int byteOffset = 0;
    var neighbourCount = filterSize * filterSize;
    int medianIndex = neighbourCount / 2;

    var blueNeighbours = new byte[neighbourCount];
    var greenNeighbours = new byte[neighbourCount];
    var redNeighbours = new byte[neighbourCount];

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            for (int filterY = -filterOffset, neighbour = 0;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++, neighbour++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    blueNeighbours[neighbour] = pixelBuffer[calcOffset];
                    greenNeighbours[neighbour] = pixelBuffer[calcOffset + greenOffset];
                    redNeighbours[neighbour] = pixelBuffer[calcOffset + redOffset];
                }
            }

            Array.Sort(blueNeighbours);
            Array.Sort(greenNeighbours);
            Array.Sort(redNeighbours);

            resultBuffer[byteOffset] = blueNeighbours[medianIndex];
            resultBuffer[byteOffset + greenOffset] = greenNeighbours[medianIndex];
            resultBuffer[byteOffset + redOffset] = redNeighbours[medianIndex];
            resultBuffer[byteOffset + alphaOffset] = maxByteValue;
        }
    }

    return resultBuffer;
}

Notice the definition of three separate byte arrays, each intended to represent a pixel neighbourhood’s pixel values related to a specific colour channel. Each neighbourhood colour channel byte array needs to be sorted according to value. The value located at the array index exactly halfway from the start and the end of the array represents the median value. When a median value has been determined, the result buffer pixel related to the source buffer pixel in terms of XY Location needs to be set.

Frog Filter 3×3 Smoothed

The sample source code defines two overloaded versions of an edge detection method. The first version is defined as an extension method targeting the Bitmap class. A FilterSize parameter is the only required parameter, intended to specify pixel neighbourhood width/height. In addition, when invoking this method optional parameters may be specified. When image noise reduction should be implemented the smoothNoise parameter should be defined as true. If resulting images are required in grayscale the last parameter, grayscale, should reflect true. The following code snippet provides the definition of the MinMaxEdgeDetection method.

public static Bitmap MinMaxEdgeDetection(this Bitmap sourceBitmap,
                                            int filterSize, 
                                            bool smoothNoise = false, 
                                            bool grayscale = false)
{
    return sourceBitmap.ToPixelBuffer()
                        .MinMaxEdgeDetection(sourceBitmap.Width, 
                                            sourceBitmap.Height, 
                                            filterSize,
                                            smoothNoise,
                                            grayscale)
                        .ToBitmap(sourceBitmap.Width, 
                                    sourceBitmap.Height);
}

The MinMaxEdgeDetection method as expressed above essentially acts as a wrapper method, invoking the overloaded version of this method, performing mapping between Bitmap objects and byte array pixel buffers.

An overloaded version of the MinMaxEdgeDetection method performs all of the tasks required in edge detection through means of minimum maximum pixel neighbourhood value subtraction. The method definition as provided by the following code snippet.

private static byte[] MinMaxEdgeDetection(this byte[] sourceBuffer,
                                          int imageWidth,
                                          int imageHeight,
                                          int filterSize,
                                          bool smoothNoise = false,
                                          bool grayscale = false)
{
    byte[] pixelBuffer = sourceBuffer;

    if (smoothNoise)
    {
        pixelBuffer = sourceBuffer.MedianFilter(imageWidth, 
                                                imageHeight, 
                                                filterSize);
    }

    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;

    int byteOffset = 0;

    byte minBlue = 0, minGreen = 0, minRed = 0;
    byte maxBlue = 0, maxGreen = 0, maxRed = 0;

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            minBlue = maxByteValue;
            minGreen = maxByteValue;
            minRed = maxByteValue;

            maxBlue = minByteValue;
            maxGreen = minByteValue;
            maxRed = minByteValue;

            for (int filterY = -filterOffset;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    minBlue = Math.Min(pixelBuffer[calcOffset], minBlue);
                    maxBlue = Math.Max(pixelBuffer[calcOffset], maxBlue);

                    minGreen = Math.Min(pixelBuffer[calcOffset + greenOffset], minGreen);
                    maxGreen = Math.Max(pixelBuffer[calcOffset + greenOffset], maxGreen);

                    minRed = Math.Min(pixelBuffer[calcOffset + redOffset], minRed);
                    maxRed = Math.Max(pixelBuffer[calcOffset + redOffset], maxRed);
                }
            }

            if (grayscale)
            {
                resultBuffer[byteOffset] = ByteVal((maxBlue - minBlue) * 0.114 + 
                                                    (maxGreen - minGreen) * 0.587 + 
                                                    (maxRed - minRed) * 0.299);

                resultBuffer[byteOffset + greenOffset] = resultBuffer[byteOffset];
                resultBuffer[byteOffset + redOffset] = resultBuffer[byteOffset];
                resultBuffer[byteOffset + alphaOffset] = maxByteValue;
            }
            else
            {
                resultBuffer[byteOffset] = (byte)(maxBlue - minBlue);
                resultBuffer[byteOffset + greenOffset] = (byte)(maxGreen - minGreen);
                resultBuffer[byteOffset + redOffset] = (byte)(maxRed - minRed);
                resultBuffer[byteOffset + alphaOffset] = maxByteValue;
            }
        }
    }

    return resultBuffer;
}

As discussed earlier, image noise reduction if required should be the first task performed. Based on parameter value the method applies a median filter to the source image buffer.

When iterating a pixel neighbourhood a comparison is performed between the currently iterated neighbouring pixel’s value and the previously determined minimum and maximum values.

When the grayscale method parameter reflects true, a grayscale algorithm is applied to the difference between the determined maximum and minimum pixel neighbourhood values.

Should the grayscale method parameter reflect false, grayscale algorithm logic will not execute. Instead, the result obtained from subtracting the determined minimum and maximum values are assigned to the relevant pixel and colour channel on the result buffer image.

Frog Filter 3×3 Smoothed

Sample Images

This article features several sample images provided as examples. All sample images were created using the sample application. All of the original source images used in generating sample images have been licensed by their respective authors to allow for reproduction here. The following section lists each original source image and related license and copyright details.

C# How to: Standard Deviation Edge Detection

Published August 8, 2015 C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Arithmetic , Image Filtering , Image Filters , Image Processing , Opensource Leave a Comment
Tags: Alpha Red Green Blue, Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, C#, Code Sample, Color Filters, Computer vision, Converting Images, Edge Detection, Extension Methods, Graphic Filters, How to, Image, Image Intensity, Image Manipulation, Image processing, Image Transform, Machine vision, Median Filter, Pixel Filters, Standard Deviation

Article Purpose

This article explores image edge detection implemented through computing pixel neighbourhood standard deviation on RGB colour images. The main sections of this article consists of a detailed explanation of the concepts related to the standard deviation edge detection algorithm and an in-depth discussion and a practical implementation through source code.

Butterfly Filter 3×3 Factor 5.0

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample application user interface exposes three filter configuration values to the end user in the form of predefined filter size values, a grayscale output flag and a variance factor. End users can configure whether filtered result images should express image edges using source image colour values or in grayscale. The filter size value specified by the user determines the number of pixels included when calculating standard deviation values.

Filter size has a direct correlation to the extend at which gradient edges will be represented in resulting images. Faint edge values require larger filter size values in order to be expressed in a resulting output image. Larger filter size values require additional computation and would thus have a longer completion time when compared to smaller filter size values.

The following screenshot captures the Standard Deviation Edge Detection sample application in action.

Standard Deviation Edge Detection

Image edge detection can be achieved through a variety of methods, each associated with particular benefits and trade offs. This article is focussed on image edge detection through implementing standard deviation calculations on a pixel neighbourhood.

Pixel Neighbourhood

Butterfly Filter 3×3 Factor 5

Pixel Neighbourhood Mean value

Mean value calculation forms a core part in calculating standard deviation. The mean value from a set of values could be considered equivalent to the value set’s average value. The average of a set of values can be calculated as the sum total of all the values in a set, divided by the number of values in the set.

Standard Deviation

From the Standard Deviation Wikipedia page we gain the following quote:

In statistics, the standard deviation (SD, also represented by the Greek letter sigma, σ for the population standard deviation or s for the sample standard deviation) is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A standard deviation close to 0 indicates that the data points tend to be very close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values

A pixel neighbourhood’s standard deviation can indicate whether a significant change in image gradient is present in a pixel neighbourhood. A large standard deviation value is an indication that the neighbourhood’s pixel values could be spread far from the calculated mean. Inversely, a small standard deviation will indicate that the neighbourhood’s pixel values are closer to the calculated mean. A sudden change in image gradient will equate to a large standard deviation.

Steps required in calculating standard deviation can be described as follows:

Calculate the Mean value. Calculate the sum of all pixels in a pixel neighbourhood then divide the sum total using the number of pixels contained in a neighbourhood. In essence calculating the mean value should be seen as calculating the average of all the pixels in a neighbourhood.
Calculate combined Variance using Mean value. Subtract the mean value from each pixel in the neighbourhood, the result should be squared and added to a sum total. Variance should then be calculated as the calculated mean subtracted squared pixel value divided using the number of pixels in a neighbourhood.
Calculate standard deviation as the Variance square root.

Butterfly Filter 3×3 Factor 5

Standard Deviation Edge Detection Algorithm

The standard deviation edge detection algorithm is based in the concept of standard deviation, providing additional capabilities. The algorithm allows for a more prominent expression of variance through means of a variance factor. Calculated variance values can be increased or decreased when implementing a variance factor. When variances are less significant, resulting images will express gradient edges at faint/low intensity levels. Providing a variance factor will result in output images expressing gradient edges at a higher intensity.

Variance factor and filter size should not be confused. When source gradient edges are expressed at low intensities, higher filter sizes would result in those low intensity source edges to be expressed in resulting images. In a scenario where high intensity gradient edges from a source image are expressed in resulting images at low intensities, a higher variance factor would increase resulting image gradient edge intensity.

The following list provides a summary of the steps required to implement the standard deviation edge detection algorithm:

Iterate through all of the pixels contained within an image.
For each pixel being iterated, determine the neighbouring pixels. The pixel neighbourhood size will be determined by the specified filter size.
Calculate the Mean value of the current pixel neighbourhood.
Calculate the Variance. Subtract the Mean value from each neighbourhood pixel, the result should be squared and summed to a variance total value. Finally, the variance total value should be divided by the number of pixels that make up the pixel neighbourhood. If a variance factor had been specified, the calculated variance value should be multiplied against it and the result assigned as the new calculated variance value.
Calculate the Standard Deviation. Once the variance has been calculated the standard deviation can be expressed as the square root of the calculated variance value. The standard deviation value should be assigned to the result buffer pixel relating to the source buffer pixel currently being iterated.

It is important to note that the steps as described above should be applied per individual colour channel, Red, Green and Blue.

Butterfly Filter 3×3 Factor 4.5

Implementing a Standard Deviation Edge Detection filter

The sample source code that accompanies this article provides a public extension method targeting the Bitmap class. A private overloaded implementation of the StandardDeviationEdgeDetection method performs the bulk of the required functionality. The following code snippet illustrates the public overloaded version of the StandardDeviationEdgeDetection method:

public static Bitmap StandardDeviationEdgeDetection(this Bitmap sourceBuffer, 
                                                    int filterSize, 
                                                    float varianceFactor = 1.0f, 
                                                    bool grayscaleOutput = true)
{
     return sourceBuffer.ToPixelBuffer()
                        .StandardDeviationEdgeDetection(sourceBuffer.Width, 
                                                        sourceBuffer.Height,
                                                        filterSize,
                                                        varianceFactor,
                                                        grayscaleOutput)
                         .ToBitmap(sourceBuffer.Width, sourceBuffer.Height);
}

The StandardDeviationEdgeDetection method accepts 3 parameters, the first Bitmap parameter serves to signal that the method is an extension method targeting the Bitmap class. A brief description of the other parameters as follows:

filterSize determines the pixel neighbourhood size. Note that the parameter is expected to reflect the pixel neighbourhood width/height. As an example, a filterSize parameter value provided as 3 would equate to a pixel neighbourhood consisting of 9 pixels, as would a filterSize of 5 indicate a neighbourhood of 25 pixels.
varianceFactor signifies the factor value applied to a calculated variance.
grayscale being a boolean value indicates whether the resulting image should be represented in grayscale, or in the original colour values from the source image.

Butterfly Filter 3×3 Factor 4

The following code snippet relates the private implementation of the StandardDeviationEdgeDetection method, which performs all of the tasks required to implement the standard deviation edge detection algorithm.

private static byte[] StandardDeviationEdgeDetection(this byte[] pixelBuffer, 
                                                     int imageWidth, 
                                                     int imageHeight,
                                                     int filterSize,
                                                     float varianceFactor = 1.0f,
                                                     bool grayscaleOutput = true)
{
    byte[] resultBuffer = new byte[pixelBuffer.Length];

    int filterOffset = (filterSize - 1) / 2;
    int calcOffset = 0;
    int stride = imageWidth * pixelByteCount;
            
    int byteOffset = 0;
    var neighbourCount = filterSize * filterSize;
            
    var blueNeighbours = new int[neighbourCount];
    var greenNeighbours = new int[neighbourCount];
    var redNeighbours = new int[neighbourCount];

    double resetValue = 0;
    double meanBlue = 0, meanGreen = 0, meanRed = 0;
    double varianceBlue = 0, varianceGreen = 0, varianceRed = 0;

    varianceFactor = varianceFactor * varianceFactor;

    for (int offsetY = filterOffset; offsetY <
        imageHeight - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            imageWidth - filterOffset; offsetX++)
        {
            byteOffset = offsetY *
                            stride +
                            offsetX * pixelByteCount;

            meanBlue = resetValue;
            meanGreen = resetValue;
            meanRed = resetValue;

            varianceBlue = resetValue;
            varianceGreen = resetValue;
            varianceRed = resetValue;

            for (int filterY = -filterOffset, neighbour = 0;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++, neighbour++)
                {
                    calcOffset = byteOffset +
                                    (filterX * pixelByteCount) +
                                    (filterY * stride);

                    blueNeighbours[neighbour] = pixelBuffer[calcOffset];
                    greenNeighbours[neighbour] = pixelBuffer[calcOffset + 1];
                    redNeighbours[neighbour] = pixelBuffer[calcOffset + 2];
                }
            }

            meanBlue = blueNeighbours.Average();
            meanGreen = greenNeighbours.Average();
            meanRed = redNeighbours.Average();

            for (int n = 0; n < neighbourCount; n++)
            {
                varianceBlue = varianceBlue + 
                                SquareNumber(blueNeighbours[n] - meanBlue);
                varianceGreen = varianceGreen + 
                                SquareNumber(greenNeighbours[n] - meanGreen);
                varianceRed = varianceRed + 
                                SquareNumber(redNeighbours[n] - meanRed);
            }

            varianceBlue = varianceBlue / 
                            neighbourCount * 
                            varianceFactor;

            varianceGreen = varianceGreen /
                            neighbourCount * 
                            varianceFactor;

            varianceRed = varianceRed / 
                            neighbourCount * 
                            varianceFactor;

            if (grayscaleOutput)
            {
                var pixelValue = ByteVal(ByteVal(Math.Sqrt(varianceBlue)) |
                                         ByteVal(Math.Sqrt(varianceGreen)) | 
                                         ByteVal(Math.Sqrt(varianceRed)));

                resultBuffer[byteOffset] = pixelValue;
                resultBuffer[byteOffset + 1] = pixelValue;
                resultBuffer[byteOffset + 2] = pixelValue;
                resultBuffer[byteOffset + 3] = Byte.MaxValue;
            }
            else
            {
                resultBuffer[byteOffset] = ByteVal(Math.Sqrt(varianceBlue));
                resultBuffer[byteOffset + 1] = ByteVal(Math.Sqrt(varianceGreen));
                resultBuffer[byteOffset + 2] = ByteVal(Math.Sqrt(varianceRed));
                resultBuffer[byteOffset + 3] = Byte.MaxValue;
            }
        }
    }

    return resultBuffer;
}

This method features several for loops, resulting in each image pixel being iterated. Notice how the two inner most loops declare negative initializer values. In order to determine a pixel’s neighbourhood, the pixel should be considered as being located at the exact center of the neighbourhood. Negative initializer values enable the code to determine neighbouring pixels located to the left and above of the pixel being iterated.

A pixel neighbourhood needs to be determined in terms of each colour channel, Red, Green and Blue. The pixel neighbourhood of each colour channel must be averaged individually. Logically it follows that pixel neighbourhood variance should also be calculated per colour channel.

The method signature indicates the varianceFactor parameter should be optional and assigned a default value of 1.0. Should a variance factor not be required, implementing a default factor value of 1.0 will not result in any change to the calculated variance value.

When grayscale output has been configured the resulting output pixel will express the same value on all three colour channels. The grayscale value will be calculated through the application of a bitwise OR operation, applied to the standard deviation of each colour channel. The square root of a pixel neighbourhood’s variance provides the standard deviation value for that pixel neighbourhood.

If grayscale output had not been configured the resulting pixel colour channels will be assigned the standard deviation of the related colour channel on the source pixel.

private const byte maxByteValue = Byte.MaxValue;
private const byte minByteValue = Byte.MinValue;

public static byte ByteVal(int val)
{
    if (val < minByteValue) { return  minByteValue; }
    else if (val > maxByteValue) { return  maxByteValue; }
    else { return (byte)val; }
}

The StandardDeviationEdgeDetection method reflects several references to the ByteVal method, as illustrated in the code snippet above. Casting double and int values to byte values could result in values exceeding the upper and lower bounds allowed by the byte type. The ByteVal method tests whether a value would exceed upper and lower bounds, when determined to do so the resulting value is assigned either the upper inclusive bound or lower inclusive bound value, depending on the bound being exceeded.

Bee Filter 3×3 Factor 5

Sample Images

C# How to: Image Distortion Blur

Published August 9, 2013 Augmented Reality , Blogging , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Filters , Image Processing , Image Transform , Microsoft , New Version , Non-Photorealistic Rendering , Opensource , Tip , Update Leave a Comment
Tags: Alpha Red Green Blue, Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Blur, C#, Code Sample, Color Filters, Computer vision, Converting Images, Extension Methods, Graphic Filters, How to, Image, Image Blur, Image Distortion, Image Intensity, Image Manipulation, Image processing, Image Transform, Machine vision, Median Filter, Morphologial Filters, Non-Photorealistic Rendering, Pixel Filters

Article Purpose

This article explores the process of implementing an Image Distortion Blur filter. This image filter is classified as a non-photo realistic image filter, primarily implemented in rendering artistic effects.

Flower: Distortion Factor 15

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Flower: Distortion Factor 10

Using the Sample Application

The sample source code that accompanies this article includes a Windows Forms based sample application. The concepts explored in this article have all been implemented as part of the sample application. From an end user perspective the following configurable options are available:

Load/Save Images – Clicking the Load Image button allows a user to specify a source/input image. If desired, output filtered images can be saved to the local file system by clicking the Save Image button.
Distortion Factor – The level or intensity of image distortion applied when implementing the filter can be specified when adjusting the Distortion Factor through the user interface. Lower factor values result in less distortion being evident in resulting images. Specifying higher factor values result in more intense image distortion being applied.

The following image is screenshot of the Image Distortion Blur sample application:

Flower: Distortion Factor 10

Flower: Distortion Factor 10

Image Distortion

In this article and the accompanying sample source code images are distorted through slightly adjusting each individual pixel’s coordinates. The direction and distance by which pixel coordinates are adjusted differ per pixel as a result of being randomly selected. The maximum distance offset applied depends on the user specified Distortion Factor. Once all pixel coordinates have been updated, implementing a Median Filter provides smoothing and an image blur effect.

Applying an Image Distortion Filter requires implementing the following steps:

Iterate Pixels – Each pixel forming part of the source/input image should be iterated.
Calculate new Coordinates – For every pixel being iterated generate two random values representing XY-coordinate offsets to be applied to a pixel’s current coordinates. Offset values can equate to less than zero in order to represent coordinates above or to the left of the current pixel.
Apply Median Filter – The newly offset pixels will appear somewhat speckled in the resulting image. Applying a Median Filter reduces the speckled appearance whilst retaining a distortion effect.

Flower: Distortion Factor 10

Median Filter

Applying a Median Filter is the final step required when implementing an Image Distortion Blur filter. Median Filters are often implemented in reducing image noise. The method of image distortion illustrated in this article express similarities when compared to image noise. In order to soften the appearance of image noise we implement a Median Filter.

A Median Filter can be applied through implementing the following steps:

Iterate Pixels – Each pixel forming part of the source/input image should be iterated.
Inspect Pixel Neighbourhood – Each neighbouring pixel in relation to the pixel currently being iterated should be added to a temporary collection.
Determine Neighbourhood Median – Once all neighbourhood pixels have been added to a temporary collection, sort the collection by value. The element value located at the middle of the collection represents the pixel neighbourhood’s Median value.

Flower: Distortion Factor 10

Flower: Distortion Factor 15

Implementing Image Distortion

The sample source code defines the DistortionBlurFilter method, an extension method targeting the Bitmap class. The following code snippet illustrates the implementation:

public static Bitmap DistortionBlurFilter( 
         this Bitmap sourceBitmap, int distortFactor) 
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = sourceBitmap.GetByteArray(); 

 
    int imageStride = sourceBitmap.Width * 4; 
    int calcOffset = 0, filterY = 0, filterX = 0; 
    int factorMax = (distortFactor + 1) * 2; 
    Random rand = new Random(); 

 
    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    {
        filterY = distortFactor - rand.Next(0, factorMax); 
        filterX = distortFactor - rand.Next(0, factorMax); 

 
        if (filterX * 4 + (k % imageStride) < imageStride  
                   && filterX * 4 + (k % imageStride) > 0) 
        { 
            calcOffset = k + filterY * imageStride +  
                         4 * filterX; 

 
            if (calcOffset >= 0 &&  
                calcOffset + 4 < resultBuffer.Length) 
            { 
                resultBuffer[calcOffset] = pixelBuffer[k]; 
                resultBuffer[calcOffset + 1] = pixelBuffer[k + 1]; 
                resultBuffer[calcOffset + 2] = pixelBuffer[k + 2]; 
            }
        }
    }

 
    return resultBuffer.GetImage(sourceBitmap.Width,  
                        sourceBitmap.Height).MedianFilter(3); 
}

Flower: Distortion Factor 15

Implementing a Median Filter

The MedianFilter extension method targets the Bitmap class. The implementation as follows:

public static Bitmap MedianFilter(this Bitmap sourceBitmap, 
                                  int matrixSize) 
{ 
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length]; 
    byte[] middlePixel; 


    int imageStride = sourceBitmap.Width * 4; 
    int filterOffset = (matrixSize - 1) / 2; 
    int calcOffset = 0, filterY = 0, filterX = 0; 
    List<int> neighbourPixels = new List<int>(); 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    { 
        filterY = -filterOffset; filterX = -filterOffset; 
        neighbourPixels.Clear(); 


        while (filterY <= filterOffset) 
        { 
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            if (calcOffset > 0 &&  
                calcOffset + 4 < pixelBuffer.Length) 
            { 
                neighbourPixels.Add(BitConverter.ToInt32( 
                                    pixelBuffer, calcOffset)); 
            } 


            filterX++; 


            if (filterX > filterOffset) 
             { filterX = -filterOffset; filterY++; }
        }


        neighbourPixels.Sort(); 
        middlePixel = BitConverter.GetBytes( 
                      neighbourPixels[filterOffset]); 


        resultBuffer[k] = middlePixel[0]; 
        resultBuffer[k + 1] = middlePixel[1]; 
        resultBuffer[k + 2] = middlePixel[2]; 
        resultBuffer[k + 3] = middlePixel[3]; 
    }


    return resultBuffer.GetImage(sourceBitmap.Width,  
                                 sourceBitmap.Height); 
}

Flower: Distortion Factor 25

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Lilium chalcedonicum in habitat at Hrisomiglia, Greece.
Attribution: Ernst Gügel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Lilium ponticum in habitat near Ikizdere, Turkey.
Attribution: Ernst Gügel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Lilium sargentiae flora.
Attribution: Denis Barthel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

A lilium longiflorum, commonly known as an Easter Lily.
Attribution: Matt H. Wade. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Flora Lilium bulbiferum ssp. croceum, ex coll. Monte Adone, Bologna, Italia.
Attribution: Denis Barthel. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Turks Cap Lily the Great Smoky Mountains National Park in western North Carolina.
Attribution: Arx Fortis. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Download from Wikipedia

Orange Lily in full bloom showing pollen covered stamens, Ontario, Canada. June 2002.
Attribution: Relic38. This file is licensed under the Creative Commons Attribution 3.0 Unported license.
Download from Wikipedia

Zantedeschia aethiopica (common names calla lily, arum lily).
Attribution: Two+two=4. This file has been released into the public domain. This applies worldwide.
Download from Wikipedia

C# How to: Image Blur

Published June 9, 2013 Augmented Reality , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Image Processing , Learn Everyday , Microsoft , New Version , Opensource , Update 29 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Box Blur, C#, Calculating Kernels, Code Sample, Converting Images, Convolution matrix, Feature extraction, Gaussian, Gaussian Blur, Gaussian Kernels, Graphic Filters, Image, Image Blur, Image processing, Image Smoothing, Image Transform, Machine vision, Matrix, Mean Filter, Median Filter, Motion Blur, Pixel Filters

Article Purpose

This article serves to provides an introduction and discussion relating to Image Blurring methods and techniques. The Image Blur methods covered in this article include: Box Blur, Gaussian Blur, Mean Filter, Median Filter and Motion Blur.

Daisy: Mean 9×9

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article is accompanied by a sample application, intended to provide a means of testing and replicating topics discussed in this article. The sample application is a Windows Forms based application of which the user interface enables the user to select an Image Blur type to implement.

When clicking the Load Image button users are able to browse the local file system in order to select source/input images. In addition users are also able to save blurred result images when clicking the Save Image button and browsing the local file system.

Daisy: Mean 7×7

The sample application provides the user with the ability to select the method of image blurring to implement. The combobox dropdown located on the right-hand side of the user interface lists all of the supported methods of image blurring. When a user selects an item from the combobox, the associated blur method will be implemented on the preview image.

The image below is a screenshot of the Image Blur Filter sample application in action:

Image Blur Overview

The process of image blurring can be regarded as reducing the sharpness or crispness defined by an image. Image blurring results in image detail/definition being perceived as less distinct. Images are often blurred as a method of smoothing an image.

Images perceived as too crisp/sharp can be softened by applying a variety of image blurring techniques and intensity levels. Often images are smoothed/blurred in order to remove/reduce image noise. In image edge detection implementations better results are often achieved when first implementing noise reduction through smoothing/blurring. Image blurring can even be implemented in a fashion where results reflect image edge detection, a method known as Difference of Gaussians.

In this article and the accompanying sample source code all methods of image blurring supported have been implemented through image convolution, with the exception of the Median filter. Each of the supported methods in essence only represent a different convolution matrix kernel. The image blurring technique capable of achieving optimal results will to varying degrees be dependent on the features present in the specified source/input image. Each method provides a different set of desired properties and compromises. In the following sections an overview of each method will be discussed.

Daisy: Mean 9×9

Mean Filter/Box Blur

The Mean Filter also sometimes referred to as a Box Blur represents a fairly simplistic implementation and definition. A Mean Filter definition can be found on Wikipedia as follows:

A box blur is an image filter in which each pixel in the resulting image has a value equal to the average value of its neighbouring pixels in the input image. It is a form of low-pass ("blurring") filter and is a convolution.

Due to its property of using equal weights it can be implemented using a much simpler accumulation algorithm which is significantly faster than using a sliding window algorithm.

Mean Filter as a title relates to all weight values in a convolution kernel being equal, therefore the alternate title of Box Blur. In most cases a Mean Filter matrix kernel will only contain the value one. When performing image convolution implementing a Mean Filter kernel, the factor value equates to the 1 being divided by the sum of all kernel values.

The following is an example of a 5×5 Mean Filter convolution kernel:

The kernel consist of 25 elements, therefore the factor value equates to one divided by twenty five.

The Mean Filter Blur does not result in the same level of smoothing achieved by other image blur methods. The Mean Filter method can also be susceptible to directional artefacts.

Daisy Mean 5×5

Gaussian Blur

The Gaussian method of image blurring is a popular and often implemented filter. In contrast to the Box Blur method Gaussian Blurring produce resulting images appearing to contain a more uniform level of smoothing. When implementing image edge detection a Gaussian Blur is often applied to source/input images resulting in noise reduction. The Gaussian Blur has a good level of image edge preservation, hence being used in edge detection operations.

From Wikipedia we gain the following description:

A Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales

A potential drawback to implementing a Gaussian blur results from the filter being computationally intensive. The following matrix kernel represents a 5×5 Gaussian Blur. The sum total of all elements in the kernel equate to 159, therefore a factor value of 1.0 / 159.0 will be implemented.

Daisy: Gaussian 5×5

Median Filter Blur

The Median Filter is classified as a non-linear filter. In contrast to the other methods of image blurring discussed in this article the Median Filter implementation does not involve convolution or a predefined matrix kernel. The following description can be found on Wikipedia:

In signal processing, it is often desirable to be able to perform some kind of noise reduction on an image or signal. The median filter is a nonlinear digital filtering technique, often used to remove noise. Such noise reduction is a typical pre-processing step to improve the results of later processing (for example, edge detection on an image). Median filtering is very widely used in digital image processing because, under certain conditions, it preserves edges while removing noise.

Daisy: Median 7×7

As the name implies, the Median Filter operates by calculating the median value of a pixel group also referred to as a window. Calculating a Median value involves a number of steps. The required steps are listed as follows:

Iterate each pixel that forms part of the source/input image.
In relation to the pixel currently being iterated determine neighbouring pixels located within the bounds defined by the window size. The window location should be offset in order to align the window’s middle pixel and the pixel currently being iterated.
Neighbouring pixels located within the bounds defined by the window should be added to a one dimensional neighbourhood array. Once all value have been added, the array should be sorted by value.
The pixel value located at the middle of the sorted neighbourhood array qualifies as the Median value. The newly determined Median value should be assigned to the pixel currently being iterated.
Repeat the steps listed above until all pixels within the source/input image have been iterated.

Similar to the Gaussian Blur filter the Median Filter has the ability to smooth image noise whilst providing edge preservation. Depending on the window size implemented and the physical dimensions of input/source images the Median Filter can be computationally expensive.

Daisy: Median 9×9

Motion Blur

The sample source implements Motion Blur filters. Motion blurring in the traditional sense has been association with photography and video capturing. Motion Blurring can often be observed in scenarios where rapid movements are being captured to photographs or video recording. When recording a single frame, rapid movements could result in the image changing before the frame being captured has completed.

Motion Blurring can be synthetically imitated through the implementation of Digital Motion Blur filters. The size of the matrix kernel provided when implementing image convolution affects the filter intensity perceived in result images. Relating to Motion Blur filters the size of the kernel specified in convolution influences the perception and appearance of how rapidly movement had occurred to have blurred the resulting image. Larger kernels produce the appearance of more rapid motion, whereas smaller kernels result in less rapid motion being perceived.

Daisy: Motion Blur 7×7 135 Degrees

Depending on the kernel specified the ability exists to create the appearance of movement having occurred in a certain direction. The sample source code implements Motion Blur filters at 45 degrees, 135 degrees and in both directions simultaneously.

The kernel listed below represents a 5×5 Motion Blur filter occurring at 45 degrees and 135 degrees:

Image Blur Implementation

The sample source code implements all of the concepts explored throughout this article. The source code definition can be grouped into 4 sections: ImageBlurFilter method, ConvolutionFilter method, MedianFilter method and the Matrix class. The following article sections relate to the 4 main source code sections.

The ImageBlurFilter extension method has the purpose of invoking the correct blur filter method and relevant method parameters. This method acts as a method wrapper providing the technical implementation details required when performing a specified blur filter.

The definition of the ImageBlurFilter extension method as follows:

 public static Bitmap ImageBlurFilter(this Bitmap sourceBitmap,  
                                             BlurType blurType) 
{  
     Bitmap resultBitmap = null; 

       
     switch (blurType) 
     {  
         case BlurType.Mean3x3: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean3x3, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.Mean5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean5x5, 1.0 / 25.0, 0); 
              } break; 
         case BlurType.Mean7x7: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean7x7, 1.0 / 49.0, 0); 
              } break; 
         case BlurType.Mean9x9: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean9x9, 1.0 / 81.0, 0); 
              } break; 
         case BlurType.GaussianBlur3x3: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                         Matrix.GaussianBlur3x3, 1.0 / 16.0, 0); 
              } break; 
         case BlurType.GaussianBlur5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                        Matrix.GaussianBlur5x5, 1.0 / 159.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                           Matrix.MotionBlur5x5, 1.0 / 10.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur5x5At45Degrees, 1.0 / 5.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur5x5At135Degrees, 1.0 / 5.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7, 1.0 / 14.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7At45Degrees, 1.0 / 7.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7At135Degrees, 1.0 / 7.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9, 1.0 / 18.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9At45Degrees, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9At135Degrees, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.Median3x3: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(3); 
              } break; 
         case BlurType.Median5x5: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(5); 
              } break; 
         case BlurType.Median7x7: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(7); 
              } break; 
         case BlurType.Median9x9: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(9); 
              } break; 
         case BlurType.Median11x11: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(11); 
              } break; 
      }  

   
     return resultBitmap; 
}

Daisy: Motion Blur 9×9

The Matrix class serves as a collection of various kernel definitions. The Matrix class and all public properties are defined as static. The definition of the Matrix class as follows:

     public static class Matrix 
    {  
         public static double[,] Mean3x3 
         {  
             get 
             {  
                 return new double[,]   
                { {  1, 1, 1, },  
                  {  1, 1, 1, },  
                  {  1, 1, 1, }, }; 
             }  
         }  

  
         public static double[,] Mean5x5 
         {  
             get 
             {  
                 return new double[,]   
                { {  1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, }; 
            }  
        }  

    
        public static double[,] Mean7x7 
        {  
             get 
             {  
                return new double[,]   
                { {  1, 1, 1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, }; 
             }  
        }  

    
         public static double[,] Mean9x9 
         {  
             get 
             {  
                return new double[,]   
                { {  1, 1, 1, 1, 1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, }; 
            }  
        }  

    
        public static double[,] GaussianBlur3x3 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 2, 1, },  
                  {  2, 4, 2, },  
                  {  1, 2, 1, }, }; 
            }  
        }  

    
        public static double[,] GaussianBlur5x5 
        {  
            get 
            {  
                return new double[,]   
                { {  2, 04, 05, 04, 2 },  
                  {  4, 09, 12, 09, 4 },  
                  {  5, 12, 15, 12, 5 }, 
                  {  4, 09, 12, 09, 4 }, 
                  {  2, 04, 05, 04, 2 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5 
        {  
             get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 1 },  
                  {  0, 1, 0, 1, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 1, 0 }, 
                  {  1, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5At45Degrees 
        {  
             get 
            {  
                return new double[,]   
                { {  0, 0, 0, 0, 1 },  
                  {  0, 0, 0, 1, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 0, 0 }, 
                  {  1, 0, 0, 0, 0 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5At135Degrees 
        {  
             get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0 },  
                  {  0, 1, 0, 0, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0 }, 
                  {  0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0, 0, 1 },  
                  {  0, 1, 0, 0, 0, 1, 0 },  
                  {  0, 0, 1, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 1, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 0, 0, 1, 0 }, 
                  {  1, 0, 0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7At45Degrees 
        {  
            get 
            {  
                return new double[,]   
                { {  0, 0, 0, 0, 0, 0, 1 },  
                  {  0, 0, 0, 0, 0, 1, 0 },  
                  {  0, 0, 0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 1, 0, 0, 0, 0 }, 
                  {  0, 1, 0, 0, 0, 0, 0 }, 
                  {  1, 0, 0, 0, 0, 0, 0 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7At135Degrees 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0, 0, 0 },  
                  {  0, 1, 0, 0, 0, 0, 0 },  
                  {  0, 0, 1, 0, 0, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 0, 0, 1, 0 }, 
                  {  0, 0, 0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9 
        {  
            get 
            {  
                return new double[,]   
                { { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9At45Degrees 
        {  
             get 
            {  
                return new double[,]   
                { { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9At135Degrees 
        {  
             get 
            {  
                return new double[,]   
                { { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, }; 
            }  
        }  
    }

Daisy: Median 7×7

The MedianFilter extension method targets the Bitmap class. The MedianFilter method applies a Median Filter using the specified Bitmap and matrix size (window size), returning a new Bitmap representing the filtered image.

The definition of the MedianFilter extension method as follows:

 public static Bitmap MedianFilter(this Bitmap sourceBitmap, 
                                   int matrixSize) 
{ 
     BitmapData sourceData = 
                sourceBitmap.LockBits(new Rectangle(0, 0, 
                sourceBitmap.Width, sourceBitmap.Height), 
                ImageLockMode.ReadOnly, 
                PixelFormat.Format32bppArgb); 

   
     byte[] pixelBuffer = new byte[sourceData.Stride * 
                                   sourceData.Height]; 

   
     byte[] resultBuffer = new byte[sourceData.Stride * 
                                    sourceData.Height]; 

   
     Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, 
                                pixelBuffer.Length); 

   
     sourceBitmap.UnlockBits(sourceData); 

   
     int filterOffset = (matrixSize - 1) / 2; 
     int calcOffset = 0; 

   
     int byteOffset = 0; 

   
     List<int> neighbourPixels = new List<int>(); 
     byte[] middlePixel; 

   
     for (int offsetY = filterOffset; offsetY < 
         sourceBitmap.Height - filterOffset; offsetY++) 
     { 
         for (int offsetX = filterOffset; offsetX < 
             sourceBitmap.Width - filterOffset; offsetX++) 
         { 
             byteOffset = offsetY * 
                          sourceData.Stride + 
                          offsetX * 4; 

   
             neighbourPixels.Clear(); 

   
             for (int filterY = -filterOffset; 
                 filterY <= filterOffset; filterY++) 
             {
                 for (int filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                 {

   
                     calcOffset = byteOffset + 
                                  (filterX * 4) + 
                                  (filterY * sourceData.Stride); 

   
                     neighbourPixels.Add(BitConverter.ToInt32( 
                                      pixelBuffer, calcOffset)); 
                 } 
             } 

   
             neighbourPixels.Sort(); 
  
             middlePixel = BitConverter.GetBytes( 
                                neighbourPixels[filterOffset]); 

   
             resultBuffer[byteOffset] = middlePixel[0]; 
             resultBuffer[byteOffset + 1] = middlePixel[1]; 
             resultBuffer[byteOffset + 2] = middlePixel[2]; 
             resultBuffer[byteOffset + 3] = middlePixel[3]; 
         } 
     }

   
     Bitmap resultBitmap = new Bitmap (sourceBitmap.Width, 
                                      sourceBitmap.Height); 

   
     BitmapData resultData = 
                resultBitmap.LockBits(new Rectangle  (0, 0, 
                resultBitmap.Width, resultBitmap.Height), 
                ImageLockMode.WriteOnly, 
                PixelFormat.Format32bppArgb); 

   
     Marshal.Copy(resultBuffer, 0, resultData.Scan0, 
                                resultBuffer.Length); 

   
     resultBitmap.UnlockBits(resultData); 

   
     return resultBitmap; 
}

Daisy: Motion Blur 9×9

The sample source code performs image convolution by invoking the ConvolutionFilter extension method.

The definition of the ConvolutionFilter extension method as follows:

private static Bitmap ConvolutionFilter(this Bitmap sourceBitmap, 
                                          double[,] filterMatrix, 
                                               double factor = 1, 
                                                    int bias = 0) 
{ 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle(0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

   
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 

   
    double blue = 0.0; 
    double green = 0.0; 
    double red = 0.0; 

   
    int filterWidth = filterMatrix.GetLength(1); 
    int filterHeight = filterMatrix.GetLength(0); 

   
    int filterOffset = (filterWidth - 1) / 2; 
    int calcOffset = 0; 

   
    int byteOffset = 0; 

   
    for (int offsetY = filterOffset; offsetY < 
        sourceBitmap.Height - filterOffset; offsetY++) 
     { 
        for (int offsetX = filterOffset; offsetX < 
            sourceBitmap.Width - filterOffset; offsetX++) 
         { 
            blue = 0; 
            green = 0; 
            red = 0; 

   
            byteOffset = offsetY * 
                         sourceData.Stride + 
                         offsetX * 4; 

   
            for (int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++) 
             { 
                for (int filterX = -filterOffset; 
                    filterX <= filterOffset; filterX++) 
                 { 

   
                    calcOffset = byteOffset + 
                                 (filterX * 4) + 
                                 (filterY * sourceData.Stride); 

   
                    blue += (double)(pixelBuffer[calcOffset]) * 
                            filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    green += (double)(pixelBuffer[calcOffset + 1]) * 
                             filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    red += (double)(pixelBuffer[calcOffset + 2]) * 
                           filterMatrix[filterY + filterOffset, 
                                              filterX + filterOffset]; 
                 } 
             }

   
            blue = factor * blue + bias; 
            green = factor * green + bias; 
            red = factor * red + bias; 

   
            blue = (blue > 255 ? 255 : 
                   (blue < 0 ? 0 : 
                    blue)); 

   
            green = (green > 255 ? 255 : 
                    (green < 0 ? 0 : 
                     green)); 

   
            red = (red > 255 ? 255 : 
                  (red < 0 ? 0 : 
                   red));  

   
            resultBuffer[byteOffset] = (byte)(blue); 
            resultBuffer[byteOffset + 1] = (byte)(green); 
            resultBuffer[byteOffset + 2] = (byte)(red); 
            resultBuffer[byteOffset + 3] = 255; 
         } 
     }

   
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 

   
    BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

   
    return resultBitmap; 
}

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction.

The sample images featuring an image of a yellow daisy is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license and can be downloaded from Wikimedia.org.

The sample images featuring an image of a white daisy is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license and can be downloaded from Wikipedia.

The sample images featuring an image of a pink daisy is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license and can be downloaded from Wikipedia.

The sample images featuring an image of a purple daisy is licensed under the Creative Commons Attribution-ShareAlike 3.0 License and can be downloaded from Wikipedia.

The Original Image

Daisy: Gaussian 3×3

Daisy: Gaussian 5×5

Daisy: Mean 3×3

Daisy: Mean 5×5

Daisy: Mean 7×7

Daisy: Mean 9×9

Daisy: Median 3×3

Daisy: Median 5×5

Daisy: Median 7×7

Daisy: Median 9×9

Daisy: Median 11×11

Daisy: Motion Blur 5×5

Daisy: Motion Blur 5×5 45 Degrees

Daisy: Motion Blur 5×5 135 Degrees

Daisy: Motion Blur 7×7

Daisy: Motion Blur 7×7 45 Degrees

Daisy: Motion Blur 7×7 135 Degrees

Daisy: Motion Blur 9×9

Daisy: Motion Blur 9×9 45 Degrees

Daisy: Motion Blur 9×9 135 Degrees

C# How to: Image Median Filter

Published May 18, 2013 Augmented Reality , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , Opensource 32 Comments
Tags: Augmented Reality, Binary Image, Bitmap, Bitmap ARGB, Bitmap ARGB Array, Bitmap Filters, Bitmap.LockBits, BitmapData, C#, Code Sample, Computer vision, Extension Methods, Image, Image Filters, Image Manipulation, Image Noise, Image processing, Median Filter, Pixel Filters, Pixel Manipulation, Signal Processing

Article purpose

The objective of this article is focussed on providing a discussion on implementing a Median Filter on an image. This article illustrates varying levels of filter intensity: 3×3, 5×5, 7×7, 9×9, 11×11 and 13×13.

Sample source code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The concepts explored in this article can be easily replicated by making use of the Sample Application, which forms part of the associated sample source code accompanying this article.

When using the Image Median Filter sample application you can specify a input/source image by clicking the Load Image button. The dropdown combobox towards the bottom middle part of the screen relates the various levels of filter intensity.

If desired a user can save the resulting filtered image to the local file system by clicking the Save Image button.

The following image is screenshot of the Image Median Filter sample application in action:

What is a Median Filter

From Wikipedia we gain the following quotes:

In signal processing, it is often desirable to be able to perform some kind of noise reduction on an image or signal. The median filter is a nonlinear digital filtering technique, often used to remove noise. Such noise reduction is a typical pre-processing step to improve the results of later processing (for example, edge detection on an image). Median filtering is very widely used in digital image processing because, under certain conditions, it preserves edges while removing noise (but see discussion below).

The main idea of the median filter is to run through the signal entry by entry, replacing each entry with the median of neighboring entries. The pattern of neighbors is called the "window", which slides, entry by entry, over the entire signal. For 1D signals, the most obvious window is just the first few preceding and following entries, whereas for 2D (or higher-dimensional) signals such as images, more complex window patterns are possible (such as "box" or "cross" patterns). Note that if the window has an odd number of entries, then the median is simple to define: it is just the middle value after all the entries in the window are sorted numerically. For an even number of entries, there is more than one possible median, see median for more details.

In simple terms, a Median Filter can be applied to images in order to achieve image smoothing or image noise reduction. The Median Filter in contrast to most image smoothing methods, to a degree exhibits edge preservation properties.

Applying a Median Filter

The sample source code defines the MedianFilter extension method targeting the Bitmap class. The matrixSize parameter determines the intensity of the Median Filter being applied.

The MedianFilter extension method iterates each pixel of the source image. When iterating image pixels we determine the neighbouring pixels of the pixel currently being iterated. After having built up a list of neighbouring pixels, the List is then sorted and from there we determine the middle pixel value. The final step involves assigning the determined middle pixel to the current pixel in the resulting image, represented as an array of pixel colour component bytes.

public static Bitmap MedianFilter(this Bitmap sourceBitmap,  
                                            int matrixSize,   
                                              int bias = 0,  
                                    bool grayscale = false)  
{
    BitmapData sourceData =  
               sourceBitmap.LockBits(new Rectangle (0, 0, 
               sourceBitmap.Width, sourceBitmap.Height), 
               ImageLockMode.ReadOnly,  
               PixelFormat.Format32bppArgb); 

  
    byte[] pixelBuffer = new byte[sourceData.Stride *  
                                  sourceData.Height]; 

  
    byte[] resultBuffer = new byte[sourceData.Stride *  
                                   sourceData.Height]; 

  
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,  
                               pixelBuffer.Length); 

  
    sourceBitmap.UnlockBits(sourceData); 

  
    if (grayscale == true) 
    { 
        float rgb = 0; 

  
        for (int k = 0; k < pixelBuffer.Length; k += 4) 
        { 
            rgb = pixelBuffer[k] * 0.11f; 
            rgb += pixelBuffer[k + 1] * 0.59f; 
            rgb += pixelBuffer[k + 2] * 0.3f; 

  
            pixelBuffer[k] = (byte )rgb; 
            pixelBuffer[k + 1] = pixelBuffer[k]; 
            pixelBuffer[k + 2] = pixelBuffer[k]; 
            pixelBuffer[k + 3] = 255; 
        } 
    } 

  
    int filterOffset = (matrixSize - 1) / 2; 
    int calcOffset = 0; 

  
    int byteOffset = 0; 
 
    List<int> neighbourPixels = new List<int>(); 
    byte[] middlePixel; 

  
    for (int offsetY = filterOffset; offsetY <  
        sourceBitmap.Height - filterOffset; offsetY++) 
    { 
        for (int offsetX = filterOffset; offsetX <  
            sourceBitmap.Width - filterOffset; offsetX++) 
        {
            byteOffset = offsetY *  
                         sourceData.Stride +  
                         offsetX * 4; 

  
            neighbourPixels.Clear(); 

  
            for (int filterY = -filterOffset;  
                filterY <= filterOffset; filterY++) 
            { 
                for (int filterX = -filterOffset; 
                    filterX <= filterOffset; filterX++) 
                { 

  
                    calcOffset = byteOffset +  
                                 (filterX * 4) +  
                        (filterY * sourceData.Stride); 

  
                    neighbourPixels.Add(BitConverter.ToInt32( 
                                     pixelBuffer, calcOffset)); 
                } 
            } 

  
            neighbourPixels.Sort(); 
 
            middlePixel = BitConverter.GetBytes( 
                               neighbourPixels[filterOffset]); 

  
            resultBuffer[byteOffset] = middlePixel[0]; 
            resultBuffer[byteOffset + 1] = middlePixel[1]; 
            resultBuffer[byteOffset + 2] = middlePixel[2]; 
            resultBuffer[byteOffset + 3] = middlePixel[3]; 
        } 
    }

  
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,  
                                     sourceBitmap.Height); 

  
    BitmapData resultData =  
               resultBitmap.LockBits(new Rectangle (0, 0, 
               resultBitmap.Width, resultBitmap.Height), 
               ImageLockMode.WriteOnly, 
               PixelFormat.Format32bppArgb); 

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,  
                               resultBuffer.Length); 

  
    resultBitmap.UnlockBits(resultData); 

  
    return resultBitmap; 
}

Sample Images

The sample images illustrated in this article were rendered from the same source image which is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license. The original image is attributed to Luc Viatour – www.Lucnix.be and can be downloaded from Wikipedia.

The Original Source Image

Median 3×3 Filter

Median 5×5 Filter

Median 7×7 Filter

Median 9×9 Filter

Median 11×11 Filter

Median 13×13 Filter

Posts Tagged 'Median Filter'

Article Purpose

Sample Source Code

Using the Sample Application

Min/Max Edge Detection

Pixel Neighbourhood

Median Filter

Min/Max Edge Detection Algorithm

Implementing a Min/Max Edge Detection Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Standard Deviation Edge Detection

Pixel Neighbourhood

Pixel Neighbourhood Mean value

Standard Deviation

Standard Deviation Edge Detection Algorithm

Implementing a Standard Deviation Edge Detection filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Image Distortion

Median Filter

Implementing Image Distortion

Implementing a Median Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article Purpose

Sample Source Code

Using the Sample Application

Image Blur Overview

Mean Filter/Box Blur

Gaussian Blur

Median Filter Blur

Motion Blur

Image Blur Implementation

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Article purpose

Sample source code

Using the Sample Application

What is a Median Filter

Applying a Median Filter

Sample Images

Related Articles and Feedback

Rate this:

Share this:

Dewald Esterhuizen

RSS Feed

Recent Posts

Blog Stats

Follow SoftwareByDefault via Email

Categories

Top Posts & Pages

Archives

C# How to Articles

SoftwareByDefault Online References

MSDN Articles

Categories

Tags