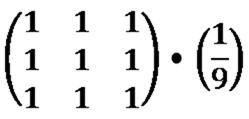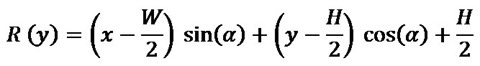Image Convolution | Software by Default

Archive for the 'Image Convolution' Category

C# How to: Fuzzy Blur Filter

Article Purpose

This article serves to illustrate the concepts involved in implementing a Fuzzy Blur Filter. This filter results in rendering non-photo realistic images which express a certain artistic effect.

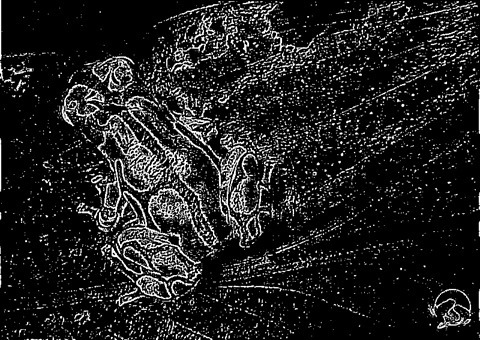
Frog: Filter Size 19×19

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

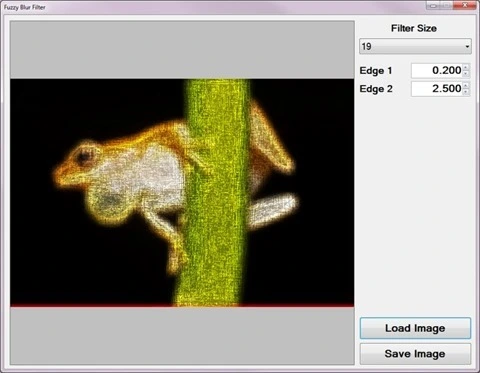
Using the Sample Application

The sample source code accompanying this article includes a Windows Forms based test application. The concepts explored throughout this article can be replicated/tested using the sample application.

When executing the sample application the user interface exposes a number of configurable options:

Loading and Saving Images – Users are able to load source/input images from the local file system by clicking the Load Image button. Clicking the Save Image button allow users to save filter result images.
Filter Size – The specified filter size affects the filter intensity. Smaller filter sizes result in less blurry images being rendered, whereas larger filter sizes result in more blurry images being rendered.
Edge Factors – The contrast of fuzzy image noise expressed in resulting images depend on the specified edge factor values. Values less than one result in detected image edges being darkened and values greater than one result in detected image edges being lightened.

The following image is a screenshot of the Fuzzy Blur Filter sample application in action:

Frog: Filter Size 9×9

Fuzzy Blur Overview

The Fuzzy Blur Filter relies on the interference of image noise when performing edge detection in order to create a fuzzy effect. In addition image blurring results from performing a mean filter.

The steps involved in performing a Fuzzy Blur Filter can be described as follows:

Edge Detection and Enhancement – Using the first edge factor specified enhance image edges by performing Boolean Edge detection. Being sensitive to image noise, a fair amount of detected image edges will actually be image noise in addition to actual image edges.
Mean Filter Blur – Using the edge enhanced image created in the previous step perform a mean filter blur. The enhanced edges will be blurred since a Mean filter does not have edge preservation properties. The size of the Mean filter implemented depends on a user specified value.
Edge Detection and Enhancement – Using the Mean filter blurred image created in the previous step once again perform Boolean Edge detection, enhancing detected edges according to the second edge factor specified.

Frog: Filter Size 9×9

Mean Filter Blurring

A Mean Filter Blur, also known as a Box Blur, can be performed through image convolution. The size of the matrix/kernel implemented when preforming image convolution will be determined through user input.

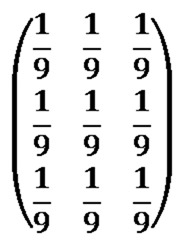
Every matrix/kernel element should be set to one. The resulting value should be multiplied by a factor value equating to one divided by the matrix/kernel size. As an example, a matrix/kernel size of 3×3 can be expressed as follows:

An alternative expression can also be:

Frog: Filter Size 9×9

Boolean Edge Detection without a local threshold

When performing Boolean Edge Detection a local threshold should be implemented in order to exclude image noise. In this article we rely on the interference of image noise in order to render a fuzzy image effect. By not implementing a local threshold when performing Boolean Edge detection the sample source code ensures sufficient interference from image noise.

The steps involved in performing Boolean Edge Detection without a local threshold can be described as follows:

Calculate Neighbourhood Mean – Iterate each pixel forming part of the source/input image. Using a 3×3 matrix size calculate the mean value of the neighbourhood surrounding the pixel currently being iterated.
Create Mean comparison Matrix – Once again using a 3×3 matrix size compare each neighbourhood pixel to the newly calculated mean value. Create a temporary 3×3 size matrix, each matrix element’s value should be the result of mean comparison. Should the value expressed by a neighbourhood pixel exceed the mean value the corresponding temporary matrix element should be set to one. When the calculated mean value exceeds the value of a neighbourhood pixel the corresponding temporary matrix element should be set to zero.
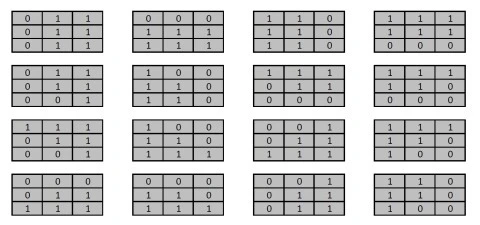
Compare Edge Masks – Using sixteen predefined edge masks compare the temporary matrix created in the previous step to each edge mask. If the temporary matrix matches one of the predefined edge masks multiply the specified factor to the pixel currently being iterated.

Note: A detailed article on Boolean Edge detection implementing a local threshold can be found here: C# How to: Boolean Edge Detection

Frog: Filter Size 9×9

The sixteen predefined edge masks each represent an image edge in a different direction. The predefined edge masks can be expressed as:

Frog: Filter Size 13×13

Implementing a Mean Filter

The sample source code defines the MeanFilter method, an extension method targeting the Bitmap class. The definition listed as follows:

private static Bitmap MeanFilter(this Bitmap sourceBitmap, 
                                 int meanSize)
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length];


    double blue = 0.0, green = 0.0, red = 0.0;
    double factor = 1.0 / (meanSize * meanSize);


    int imageStride = sourceBitmap.Width * 4;
    int filterOffset = meanSize / 2; 
    int calcOffset = 0, filterY = 0, filterX = 0; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4)
    {
        blue = 0; green = 0; red = 0;
        filterY = -filterOffset;
        filterX = -filterOffset;


        while (filterY <= filterOffset)
        {
            calcOffset = k + (filterX * 4) +
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 :
            (calcOffset >= pixelBuffer.Length - 2 ?
            pixelBuffer.Length - 3 : calcOffset));


            blue += pixelBuffer[calcOffset];
            green += pixelBuffer[calcOffset + 1];
            red += pixelBuffer[calcOffset + 2];


            filterX++;


            if (filterX > filterOffset)
            {
                filterX = -filterOffset;
                filterY++;
            }
        }


        resultBuffer[k] = ClipByte(factor * blue);
        resultBuffer[k + 1] = ClipByte(factor * green);
        resultBuffer[k + 2] = ClipByte(factor * red);
        resultBuffer[k + 3] = 255;
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height);
}

Frog: Filter Size 19×19

Implementing Boolean Edge Detection

Boolean Edge detection is performed in the sample source code through the implementation of the BooleanEdgeDetectionFilter method. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the BooleanEdgeDetectionFilter extension method:

public static Bitmap BooleanEdgeDetectionFilter( 
       this Bitmap sourceBitmap, float edgeFactor) 
{
    byte[] pixelBuffer = sourceBitmap.GetByteArray(); 
    byte[] resultBuffer = new byte[pixelBuffer.Length]; 
    Buffer.BlockCopy(pixelBuffer, 0, resultBuffer, 
                     0, pixelBuffer.Length); 


    List<string> edgeMasks = GetBooleanEdgeMasks(); 
 
    int imageStride = sourceBitmap.Width * 4; 
    int matrixMean = 0, pixelTotal = 0; 
    int filterY = 0, filterX = 0, calcOffset = 0; 
    string matrixPatern = String.Empty; 


    for (int k = 0; k + 4 < pixelBuffer.Length; k += 4) 
    {
        matrixPatern = String.Empty; 
        matrixMean = 0; pixelTotal = 0; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 
 
            matrixMean += pixelBuffer[calcOffset]; 
            matrixMean += pixelBuffer[calcOffset + 1]; 
            matrixMean += pixelBuffer[calcOffset + 2]; 


            filterX += 1; 


            if (filterX > 1) 
             { filterX = -1; filterY += 1; } 
        }


        matrixMean = matrixMean / 9; 
        filterY = -1; filterX = -1; 


        while (filterY < 2) 
        {
            calcOffset = k + (filterX * 4) + 
            (filterY * imageStride); 


            calcOffset = (calcOffset < 0 ? 0 : 
            (calcOffset >= pixelBuffer.Length - 2 ? 
            pixelBuffer.Length - 3 : calcOffset)); 


            pixelTotal = pixelBuffer[calcOffset]; 
            pixelTotal += pixelBuffer[calcOffset + 1]; 
            pixelTotal += pixelBuffer[calcOffset + 2]; 
 
            matrixPatern += (pixelTotal > matrixMean 
                                       ? "1" : "0"); 
            filterX += 1; 


            if (filterX > 1) 
            { filterX = -1; filterY += 1; } 
        } 


        if (edgeMasks.Contains(matrixPatern)) 
        {
            resultBuffer[k] = 
            ClipByte(resultBuffer[k] * edgeFactor); 


            resultBuffer[k + 1] = 
            ClipByte(resultBuffer[k + 1] * edgeFactor); 


            resultBuffer[k + 2] = 
            ClipByte(resultBuffer[k + 2] * edgeFactor); 
        }
    }


    return resultBuffer.GetImage(sourceBitmap.Width, sourceBitmap.Height); 
}

Frog: Filter Size 13×13

The predefined edge masks implemented in mean comparison have been wrapped by the GetBooleanEdgeMasks method. The definition as follows:

public static List<string> GetBooleanEdgeMasks() 
{
    List<string> edgeMasks = new List<string>(); 


    edgeMasks.Add("011011011"); 
    edgeMasks.Add("000111111"); 
    edgeMasks.Add("110110110"); 
    edgeMasks.Add("111111000"); 
    edgeMasks.Add("011011001"); 
    edgeMasks.Add("100110110"); 
    edgeMasks.Add("111011000"); 
    edgeMasks.Add("111110000"); 
    edgeMasks.Add("111011001"); 
    edgeMasks.Add("100110111"); 
    edgeMasks.Add("001011111"); 
    edgeMasks.Add("111110100"); 
    edgeMasks.Add("000011111"); 
    edgeMasks.Add("000110111"); 
    edgeMasks.Add("001011011"); 
    edgeMasks.Add("110110100"); 


    return edgeMasks; 
}

Frog: Filter Size 19×19

Implementing a Fuzzy Blur Filter

The FuzzyEdgeBlurFilter method serves as the implementation of a Fuzzy Blur Filter. As discussed earlier a Fuzzy Blur Filter involves enhancing image edges through Boolean Edge detection, performing a Mean Filter blur and then once again performing Boolean Edge detection. This method has been defined as an extension method targeting the Bitmap class.

The following code snippet provides the definition of the FuzzyEdgeBlurFilter method:

public static Bitmap FuzzyEdgeBlurFilter(this Bitmap sourceBitmap,  
                                         int filterSize,  
                                         float edgeFactor1,  
                                         float edgeFactor2) 
{
    return  
    sourceBitmap.BooleanEdgeDetectionFilter(edgeFactor1). 
    MeanFilter(filterSize).BooleanEdgeDetectionFilter(edgeFactor2); 
}

Frog: Filter Size 3×3

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following images feature as sample images:

Tyler’s Tree Frog
Attribution: LiquidGhoul. This file has been released into the public domain by its author, LiquidGhoul. This applies worldwide.
Download from Wikipedia.

Phyllobates Terribilis
Attribution: Wilfried Berns. This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Germany license.
Download from Wikipedia.

Dendropsophus Microcephalus
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia

Panamanian Golden Frog
Attribution: Brian Gratwicke. This file is licensed under the Creative Commons Attribution 2.0 Generic license.
Download from Wikipedia.

C# How to: Weighted Difference of Gaussians

Published July 14, 2013 Augmented Reality , Blogging , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Arithmetic , Image Convolution , Image Filters , Image Processing , Learn Everyday , Microsoft , New Version , Opensource , Tip , Update 6 Comments
Tags: Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, C#, Calculate Matrix, Calculating Kernels, Code Sample, Computer vision, Converting Images, Difference of Gaussians, Edge Detect, Edge Detection, Feature extraction, Gaussian, Gaussian Blur, Gaussian Kernels, Graphic Filters, Image, Image Intensity, Image processing, Image Transform, Machine vision, Pixel Filters

Article Purpose

It is the purpose of this article to illustrate the concept of Difference of Gaussians Edge Detection. This article extends the conventional implementation of Difference of Gaussian algorithms through the application of equally sized matrix kernels only differing by a weight factor.

Frog: Kernel 5×5, Weight1 0.1, Weight2 2.1

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article relies on a sample application included as part of the accompanying sample source code. The sample application serves as a practical implementation of the concepts explored throughout this article.

The sample application user interface enables the user to configure and control the implementation of a Difference of Gaussians Edge Detection Image filter. The configuration options exposed through the sample application’s user interface can be detailed as follows:

Load/Save Images – When executing the sample application users are able to load source/input images from the local file system through clicking the Load Image button. If desired, the sample application enables users to save resulting images to the local file system through clicking the Save Image button.
Kernel Size – This option relates to the size of the matrix kernels that is to be implemented when performing Gaussian Blurring through image convolution. Smaller matrix kernels are faster to compute and generally result in image edges detected in the source/input image to be expressed through thinner gradient edges. Larger matrix kernels can be computationally expensive to compute as kernel sizes increase. In addition, the edges detected in source/input images will generally be expressed as thicker gradient edges in resulting images.
Weight Values – The sample application calculates Gaussian matrix kernels and in doing so implements a weight factor. A Weight Factor determines the blur intensity observed in result images after having applied image convolution. Higher weight factors result in a more intense level of Gaussian Blurring being applied. As expected, lower weight factors values result in a less intense level of Gaussian Blurring being applied. If the value of the first weight factor exceeds the value of the second weight factor resulting images will be generated with a Black background and edges being indicated in White. In a similar fashion, when the second weight factor value exceeds that of the first weight factor resulting images will be generated with a White background and edges being indicated in Black. The greater the difference between the first and second weight factor values result in a greater degree of image noise removal. When weight factor values only differ slightly, resulting images may be prone to image noise.

The following image is screenshot of the Weighted Difference of Gaussians sample application in action:

Frog: Kernel 5×5, Weight1 1.8, Weight2 0.1

Gaussian Blur

The Gaussian Blur algorithm can be described as one of the most popular and widely implemented methods of image blurring. From Wikipedia we gain the following excerpt:

A Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales.

Mathematically, applying a Gaussian blur to an image is the same as convolving the image with a Gaussian function. This is also known as a two-dimensional Weierstrass transform.

Take Note: The Gaussian Blur algorithm has the attribute of smoothing image detail/definition whilst also having an edge preservation attribute. When applying a Gaussian Blur to an image a level of image detail/definition will be blurred/smoothed away, done in a fashion that would exclude/preserve image gradient edges.

Frog: Kernel 5×5, Weight1 2.7, Weight2 0.1

Difference of Gaussians Edge Detection

Difference of Gaussian refers to a specific method of image edge detection. Difference of Gaussians, common abbreviated as DoG, functions through the implementation of Gaussian Image Blurring.

A clear and concise description can be found on the Difference of Gaussians Wikipedia Article Page:

In imaging science, difference of Gaussians is a feature enhancement algorithm that involves the subtraction of one blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing standard deviations. Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the difference of Gaussians is a band-pass filter that discards all but a handful of spatial frequencies that are present in the original grayscale image.

In a conventional sense Difference of Gaussians involves applying Gaussian Blurring to images created as copies of the original source/input image. There must be a difference in the size of the kernels implemented when applying image convolution. A typical example would be applying a 3×3 Gaussian blur on one image copy whilst applying a 5×5 Gaussian blur on another image copy. The final step requires creating a result image populated by subtracting the two blurred image copies. The results obtained from subtraction represents the edges forming part of the source/input image.

This article extends beyond the conventional method of implementing Difference of Gaussians Edge Detection. The implementation illustrated in this article retains the core concept of subtracting values which have been blurred to different intensities. The implementation method explored here differs from the conventional method in the sense that the matrix kernels implemented do not differ in size. Both matrix kernels are in fact required to have the same size dimensions.

The matrix kernels implemented are equal in terms of their size dimensions, although kernel values are different. Expressed from another angle: equally sized matrix kernels of which one represents a more intense level of blurring than the other. A matrix kernels’ resulting intensity can be determined by the weight factor implemented when calculating the kernel values.

Frog: Kernel 5×5, Weight1 3.7, Weight2 0.2

The advantages of implementing equally sized kernels can be described as follows:

Single Convolution implementation: Image Convolution involves executing several nested code loops. Application performance can be severely negatively impacted when executing large nested loops. The conventional method of implementing Difference of Gaussians generally involves having to implement two instances of image convolution, once per image copy. The Difference of Gaussians method implemented in this article executes the code loops related to image convolution only once. Considering the kernels are equal in size, both can be iterated within the same set of loops.

Eliminating Image subtraction: In conventional Difference of Gaussians implementations images expressing differing intensity levels of Gaussian Blurring have to be subtracted. The Difference of Gaussian implementation method described in this article eliminates the need to perform image subtraction. When applying image convolution using both kernels simultaneously the two results obtained, one from each kernel, can be subtracted and assigned to the result image. In addition, through calculating both kernel results at the same time further reduces the need to create two temporary source image copies.

Frog: Kernel 5×5, Weight1 2.4, Weight2 0.3

Difference of Gaussians Edge Detection Required Steps

When implementing a Difference of Gaussians Edge Detection several steps are required, those steps are detailed as follows:

Calculate Kernels – Before implementing image convolution two matrix kernels have to be calculated. The calculated kernels are required to be of equal size and differ in Gaussian Blur intensity. The sample application allows the user to configure kernel intensity through updating the weight values, expressed as Weight 1 and Weight 2.
Convert Source Image to Grayscale – Applying image convolution on grayscale images outperforms convolution on RGB images. When converting an RGB pixel to a grayscale pixel, colour components are combined to form a single gray level intensity. In other words a grayscale image consists of a third of the number of pixels when compared to the RGB image from which the grayscale image had been rendered. In the case of an ARGB image the derived grayscale image will be expressed in 25% of the number of pixels forming part of the source ARGB image. When applying image convolution the number of processor cycles increases when the image pixel count increases.
Perform Convolution Implementing Thresholds – Using the newly created grayscale image perform image convolution for both kernels calculated in the first step. The result value equates to subtracting the two results obtained from convolution. If the result value exceeds the difference between the first and second kernel weight value, the resulting pixel should be set to White, if not, set the result pixel to Black.

Frog: Kernel 5×5, Weight1 2.1, Weight2 0.5

Calculating Gaussian Convolution Kernels

The sample application implements Gaussian Blur Kernel calculations. The matrix kernels implemented in image convolution are calculated at runtime, as opposed to being hard coded. Being able to dynamically construct convolution kernels has the advantage of providing a greater degree of control in runtime regarding image convolution application.

Several steps are involved in calculating Gaussian Blur Matrix Kernels. The first required step being to determine the Matrix Kernel Size and Weight. The size and weight factor of a matrix kernel comprises the two configurable values implemented when calculating Gaussian Blur Kernels. In the case of this article and the sample application those values will be configured by the user through the sample application’s user interface.

The formula implemented in calculating Gaussian Blur Kernels can be expressed as follows:

The formula contains a number of symbols, which define how the filter will be implemented. The symbols forming part of the Gaussian Kernel formula are described in the following list:

G(x y) – A value calculated using the Gaussian Kernel formula. This value forms part of a Kernel, representing a single element.
π – Pi, one of the better known members of the Greek alphabet. The mathematical constant defined as 22 / 7.
σ – The lower case version of the Greek alphabet letter Sigma. This symbol simply represents a threshold or factor value, as specified by the user.
e – The formula references a lower case e symbol. The symbol represents Euler’s number. The value of Euler’s number has been defined as a mathematical constant equating to 2.71828182846.
x, y – The variables referenced as x and y relate to pixel coordinates within an image. y Representing the vertical offset or row and x represents the horizontal offset or column.

Note: The formula’s implementation expects x and y to equal zero values when representing the coordinates of the pixel located in the middle of the kernel.

Frog: Kernel 7×7, Weight1 0.1, Weight2 2.0

Implementing Gaussian Kernel Calculations

The sample application defines the GaussianCalculator.Calculate method. This method accepts two parameters, kernel size and kernel weight. The following code snippet details the implementation:

public static double[,] Calculate(int lenght, double weight) 
{
    double[,] Kernel = new double [lenght, lenght]; 
    double sumTotal = 0; 

  
    int kernelRadius = lenght / 2; 
    double distance = 0; 

  
    double calculatedEuler = 1.0 /  
    (2.0 * Math.PI * Math.Pow(weight, 2)); 

  
    for (int filterY = -kernelRadius; 
         filterY <= kernelRadius; filterY++) 
    {
        for (int filterX = -kernelRadius; 
            filterX <= kernelRadius; filterX++) 
        {
            distance = ((filterX * filterX) +  
                       (filterY * filterY)) /  
                       (2 * (weight * weight)); 

  
            Kernel[filterY + kernelRadius,  
                   filterX + kernelRadius] =  
                   calculatedEuler * Math.Exp(-distance); 

  
            sumTotal += Kernel[filterY + kernelRadius,  
                               filterX + kernelRadius]; 
        } 
    } 

  
    for (int y = 0; y < lenght; y++) 
    { 
        for (int x = 0; x < lenght; x++) 
        { 
            Kernel[y, x] = Kernel[y, x] *  
                           (1.0 / sumTotal); 
        } 
    } 

  
    return Kernel; 
}

Frog: Kernel 3×3, Weight1 0.1, Weight2 1.8

Implementing Difference of Gaussians Edge Detection

The sample source code defines the DifferenceOfGaussianFilter method. This method has been defined as an extension method targeting the Bitmap class. The following code snippet provides the implementation:

public static Bitmap DifferenceOfGaussianFilter(this Bitmap sourceBitmap,  
                                                int matrixSize, double weight1, 
                                                double weight2) 
{
    double[,] kernel1 =  
    GaussianCalculator.Calculate(matrixSize,  
    (weight1 > weight2 ? weight1 : weight2)); 

 
    double[,] kernel2 =  
    GaussianCalculator.Calculate(matrixSize,  
    (weight1 > weight2 ? weight2 : weight1)); 

 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle (0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly, 
                                         PixelFormat.Format32bppArgb); 

 
    byte[] pixelBuffer = new byte [sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte [sourceData.Stride * sourceData.Height]; 
    byte[] grayscaleBuffer = new byte [sourceData.Width * sourceData.Height]; 

 
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 

 
    double rgb = 0; 

 
    for (int source = 0, dst = 0;  
         source < pixelBuffer.Length && dst < grayscaleBuffer.Length;  
         source += 4, dst++) 
    { 
        rgb = pixelBuffer * 0.11f; 
        rgb += pixelBuffer * 0.59f; 
        rgb += pixelBuffer * 0.3f; 

 
        grayscaleBuffer[dst] = (byte)rgb; 
    }

 
    double color1 = 0.0; 
    double color2 = 0.0; 

 
    int filterOffset = (matrixSize - 1) / 2; 
    int calcOffset = 0; 

 
    for (int source = 0, dst = 0;  
         source < grayscaleBuffer.Length && dst + 4 < resultBuffer.Length;  
         source++, dst += 4) 
    { 
        color1 = 0; 
        color2 = 0; 

         
        for (int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++) 
        {
            for (int filterX = -filterOffset; 
                filterX <= filterOffset; filterX++) 
            {
                calcOffset = source + (filterX) + 
                             (filterY * sourceBitmap.Width); 

 
                calcOffset = (calcOffset < 0 ? 0 :  
                             (calcOffset >= grayscaleBuffer.Length ?  
                             grayscaleBuffer.Length - 1 : calcOffset)); 

 
                color1 += (grayscaleBuffer[calcOffset]) * 
                           kernel1[filterY + filterOffset, 
                           filterX + filterOffset]; 

 
                color2 += (grayscaleBuffer[calcOffset]) * 
                           kernel2[filterY + filterOffset, 
                           filterX + filterOffset]; 
            } 
        }

 
        color1 = color1 - color2; 
        color1 = (color1 >= weight1 - weight2 ? 255 : 0); 

 
        resultBuffer[dst] = (byte)color1; 
        resultBuffer[dst + 1] = (byte)color1; 
        resultBuffer[dst + 2] = (byte)color1; 
        resultBuffer[dst + 3] = 255; 
    }

 
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 

 
    BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 

 
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

 
    return resultBitmap; 
}

Frog: Kernel 3×3, Weight1 2.1, Weight2 0.7

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following image files feature as sample images:

Panamanian Golden Frog – Licensed under the Creative Commons Attribution 2.0 Generic license. Attribution: Brian Gratwicke. Download from Wikipedia.
Dendropsophus Microcephalus – Licensed under the Creative Commons Attribution 2.0 Generic license. Attribution: Brian Gratwicke. Download from Wikipedia.
Tyler’s Tree Frog – Has been released into the public domain by its author, LiquidGhoul. This applies worldwide. Download from Wikipedia.
Mimic Poison Frog – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from Wikipedia.
Phyllobates Terribilis – This file is licensed under the Creative Commons Attribution-Share Alike 2.0 Germany license. Attribution: Wilfried Berns. Download from Wikipedia.

Panamanian Golden Frog

Dendropsophus Microcephalus

Tyler’s Tree Frog

Mimic Poison Frog

Phyllobates Terribilis

C# How to: Compass Edge Detection

Published June 22, 2013 Augmented Reality , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Image Processing , Learn Everyday , Microsoft , New Version , Opensource , Tip , Update 29 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, BitmapData.Stride, Code Sample, Compass Edges, Compass Kernels, Converting Images, Edge Detection, Feature extraction, Graphic Filters, Image, Image Algorithms, Image Edge Detection, Image processing, Isotropic, Kirsch, Machine vision, Pixel Filters, Prewitt, Rotate Kernel, Rotate Transform, Scharr, Sobel

Article Purpose

This article’s objective is to illustrate concepts relating to Compass Edge Detection. The edge detection methods implemented in this article include: Prewitt, Sobel, Scharr, Kirsch and Isotropic.

Wasp: Scharr 3 x 3 x 8

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample source code accompanying this article includes a Windows Forms based sample application. When using the sample application users are able to load source/input images from and save result images to the local file system. The user interface provides a combobox which contains the supported methods of Compass Edge Detection. Selecting an item from the combobox results in the related Compass Edge Detection method being applied to the current source/input image. Supported methods are:

Prewitt3x3x4 – 3×3 Prewitt kernels in 4 compass directions
Prewitt3x3x8 – 3×3 Prewitt kernels in 8 compass directions
Prewitt5x5x4 – 5×5 Prewitt kernels in 4 compass directions
Sobel3x3x4 – 3×3 Sobel kernels in 4 compass directions
Sobel3x3x8 – 3×3 Sobel kernels in 8 compass directions
Sobel5x5x4 – 5×5 Sobel kernels in 4 compass directions
Scharr3x3x4 – 3×3 Scharr kernels in 4 compass directions
Scharr3x3x8 – 3×3 Scharr kernels in 8 compass directions
Scharr5x5x4 – 5×5 Scharr kernels in 4 compass directions
Kirsch3x3x4 – 3×3 Kirsch kernels in 4 compass directions
Kirsch3x3x8 – 3×3 Kirsch kernels in 8 compass directions
Isotropic3x3x4 – 3×3 Isotropic kernels in 4 compass directions
Isotropic3x3x8 – 3×3 Isotropic kernels in 8 compass directions

The following image is a screenshot of the Compass Edge Detection Sample Application in action:

Bee: Isotropic 3 x 3 x 8

Compass Edge Detection Overview

Compass Edge Detection as a concept title can be explained through the implementation of compass directions. Compass Edge Detection can be implemented through image convolution, using multiple matrix kernels, each suited to detecting edges in a specific direction. Often the edge directions implemented are:

North
North East
East
South East
South
South West
West
North West

Each of the compass directions listed above differ by 45 degrees. Applying a kernel rotation of 45 degrees to an existing direction specific edge detection kernel results in a new kernel suited to detecting edges in the next compass direction.

Various edge detection kernels can be implemented in Compass Edge Detection. This article and accompanying sample source code implements the following kernel types:

Prewitt
Sobel
Kirsch
Scharr
Isotropic

Prey Mantis: Sobel 3 x 3 x 8

The steps required when implementing Compass Edge Detection can be described as follows:

Determine the compass kernels. When an edge detection kernel suited to a specific direction is known, the edge detection kernels suited to the 7 remaining compass directions can be calculated. Rotating a kernel by 45 degrees around a central axis equates to the kernel suited to the next compass direction. As an example, if the edge detection kernel suited to detect edges in a northerly direction were to be rotated clockwise by 45 degrees around a central axis the result would be an edge detection kernel suited to edges in a North Easterly direction.
Iterate source image pixels. Every pixel forming part of the source/input image should be iterated, implementing convolution using each of the compass kernels.
Determine the most responsive kernel convolution. After having applied each compass kernel to the pixel currently being iterated, the most responsive compass kernel determines the output value. In other words, after having applied convolution eight times on the same pixel using each compass direction the output value should be set to the highest value calculated.
Validate and set output result. Ensure that the highest value returned from convolution does not equate to less than 0 or more than 255. Should a value be less than zero the result should be assigned as zero. In a similar fashion, should a value exceed 255 the result should be assigned as 255.

Prewitt Compass Kernels

LadyBug: Prewitt 3 x 3 x 8

Rotating Convolution Kernels

Kernels can be rotated by implementing a rotate transform. Repeatedly rotating by 45 degrees results in calculating 8 kernels, each suited to a different direction. The algorithm implemented when performing a rotate transform can be expressed as follows:

Rotate Horizontal Algorithm

Rotate Vertical Algorithm

I’ve published an in-depth article on matrix rotation available here: C# How to: Image Transform Rotate

Butterfly: Sobel 3 x 3 x 8

Implementing Kernel Rotation

The sample source code defines the RotateMatrix method. This method accepts as parameter a single kernel, defined as a two dimensional array of type double. In addition the method also expects as a parameter the degree to which the specified kernel should be rotated. The definition as follows:

public static double[, ,] RotateMatrix(double[,] baseKernel,  
                                             double degrees) 
{
    double[, ,] kernel = new double[(int )(360 / degrees),  
        baseKernel.GetLength(0), baseKernel.GetLength(1)]; 

 
    int xOffset = baseKernel.GetLength(1) / 2; 
    int yOffset = baseKernel.GetLength(0) / 2; 

 
    for (int y = 0; y < baseKernel.GetLength(0); y++) 
    { 
        for (int x = 0; x < baseKernel.GetLength(1); x++) 
        { 
            for (int compass = 0; compass <  
                kernel.GetLength(0); compass++) 
            { 
                double radians = compass * degrees * 
                                 Math.PI / 180.0; 

 
                int resultX = (int)(Math.Round((x - xOffset) * 
                           Math.Cos(radians) - (y - yOffset) * 
                           Math.Sin(radians)) + xOffset); 

 
                int resultY = (int )(Math.Round((x - xOffset) * 
                            Math.Sin(radians) + (y - yOffset) * 
                            Math.Cos(radians)) + yOffset); 

 
                kernel[compass, resultY, resultX] = 
                                            baseKernel[y, x]; 
            } 
        } 
    }

 
    return kernel; 
}

Butterfly: Prewitt 3 x 3 x 8

Implementing Compass Edge Detection

The sample source code defines several kernels which are implemented in convolution. The following code snippet provides the definition of all kernels defined:

public static double[, ,] Prewitt3x3x4 
{
    get 
    {
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -1,  0,  1,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Prewitt3x3x8 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -1,  0,  1,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 45); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Prewitt5x5x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -2, -1,  0,  1, 2,  },  
           {  -2, -1,  0,  1, 2,  }, 
           {  -2, -1,  0,  1, 2,  }, 
           {  -2, -1,  0,  1, 2,  },  
           {  -2, -1,  0,  1, 2,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Kirsch3x3x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -3, -3,  5,  },  
           {  -3,  0,  5,  },  
           {  -3, -3,  5,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Kirsch3x3x8 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -3, -3,  5,  },  
           {  -3,  0,  5,  },  
           {  -3, -3,  5,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 45); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Sobel3x3x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -2,  0,  2,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Sobel3x3x8 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -2,  0,  2,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 45); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Sobel5x5x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {   -5,  -4,  0,   4,  5,  },  
           {   -8, -10,  0,  10,  8,  }, 
           {  -10, -20,  0,  20, 10,  }, 
           {   -8, -10,  0,  10,  8,  },  
           {   -5,  -4,  0,   4,  5,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Scharr3x3x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -3,  0,  3,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Scharr3x3x8 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {  -1,  0,  1,  },  
           {  -3,  0,  3,  },  
           {  -1,  0,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 45); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Scharr5x5x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {   -1,  -1,  0,   1,  1,  },  
           {   -2,  -2,  0,   2,  2,  }, 
           {   -3,  -6,  0,   6,  3,  }, 
           {   -2,  -2,  0,   2,  2,  },  
           {   -1,  -1,  0,   1,  1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Isotropic3x3x4 
{  
    get 
    {  
        double[,] baseKernel = new double[,]  
         { {             -1,  0,             1,  },  
           {  -Math.Sqrt(2),  0,  Math.Sqrt(2),  },  
           {             -1,  0,             1,  },  }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 90); 

 
        return kernel; 
    }  
}  

 
public static double[, ,] Isotropic3x3x8 
{  
    get 
     {  
        double[,] baseKernel = new double[,]  
         { {             -1,  0,             1,  },  
           {  -Math.Sqrt(2),  0,  Math.Sqrt(2),  },  
           {             -1,  0,             1,  }, }; 

 
        double[, ,] kernel = RotateMatrix(baseKernel, 45); 

  
        return kernel; 
    }  
}

Notice how each property invokes the RotateMatrix method discussed in the previous section.

Butterfly: Scharr 3 x 3 x 8

The CompassEdgeDetectionFilter method is defined as an extension method targeting the Bitmap class. The purpose of this method is to act as a wrapper method encapsulating the technical implementation. The definition as follows:

public static Bitmap CompassEdgeDetectionFilter(this Bitmap sourceBitmap,  
                                    CompassEdgeDetectionType compassType) 
{ 
    Bitmap resultBitmap = null; 

 
    switch (compassType) 
    {
        case CompassEdgeDetectionType.Sobel3x3x4: 
             { 
                resultBitmap =  
                sourceBitmap.ConvolutionFilter(Matrix.Sobel3x3x4, 1.0 / 4.0); 
             } break; 
        case CompassEdgeDetectionType.Sobel3x3x8: 
             { 
                resultBitmap =  
                sourceBitmap.ConvolutionFilter(Matrix.Sobel3x3x8, 1.0/ 4.0); 
             } break; 
        case CompassEdgeDetectionType.Sobel5x5x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Sobel5x5x4, 1.0/ 84.0); 
             } break; 
        case CompassEdgeDetectionType.Prewitt3x3x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Prewitt3x3x4, 1.0 / 3.0); 
             } break; 
        case CompassEdgeDetectionType.Prewitt3x3x8: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Prewitt3x3x8, 1.0/ 3.0); 
             } break; 
        case CompassEdgeDetectionType.Prewitt5x5x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Prewitt5x5x4, 1.0 / 15.0); 
             } break; 
        case CompassEdgeDetectionType.Scharr3x3x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Scharr3x3x4, 1.0 / 4.0); 
             } break; 
        case CompassEdgeDetectionType.Scharr3x3x8: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Scharr3x3x8, 1.0 / 4.0); 
             } break; 
        case CompassEdgeDetectionType .Scharr5x5x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Scharr5x5x4, 1.0 / 21.0); 
             } break; 
        case CompassEdgeDetectionType.Kirsch3x3x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Kirsch3x3x4, 1.0 / 15.0); 
             } break; 
        case CompassEdgeDetectionType.Kirsch3x3x8: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Kirsch3x3x8, 1.0 / 15.0); 
             } break; 
        case CompassEdgeDetectionType.Isotropic3x3x4: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Isotropic3x3x4, 1.0 / 3.4); 
             } break; 
        case CompassEdgeDetectionType.Isotropic3x3x8: 
             { 
                resultBitmap = 
                sourceBitmap.ConvolutionFilter(Matrix.Isotropic3x3x8, 1.0 / 3.4); 
             } break; 
     } 

 
    return resultBitmap; 
}

Rose: Scharr 3 x 3 x 8

Notice from the code snippet listed above, each case statement invokes the ConvolutionFilter method. This method has been defined as an extension method targeting the Bitmap class. The ConvolutionFilter extension method performs the actual task of image convolution. This method implements each kernel passed as a parameter, the highest result value will be determined as the output value. The definition as follows:

private static Bitmap ConvolutionFilter(this Bitmap sourceBitmap,  
                                     double[,,] filterMatrix,  
                                           double factor = 1,  
                                                int bias = 0)  
{
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle(0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly,  
                                         PixelFormat.Format32bppArgb); 


    byte[] pixelBuffer = new byte [sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte [sourceData.Stride * sourceData.Height]; 


    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 


    double blue = 0.0; 
    double green = 0.0; 
    double red = 0.0; 


    double blueCompass = 0.0; 
    double greenCompass = 0.0; 
    double redCompass = 0.0; 


    int filterWidth = filterMatrix.GetLength(1); 
    int filterHeight = filterMatrix.GetLength(0); 


    int filterOffset = (filterWidth-1) / 2; 
    int calcOffset = 0; 


    int byteOffset = 0; 


    for (int offsetY = filterOffset; offsetY <  
        sourceBitmap.Height - filterOffset; offsetY++) 
     {
        for (int offsetX = filterOffset; offsetX <  
            sourceBitmap.Width - filterOffset; offsetX++) 
         {
            blue = 0; 
            green = 0; 
            red = 0; 


            byteOffset = offsetY *  
                         sourceData.Stride +  
                         offsetX * 4; 


            for (int compass = 0; compass <  
                 filterMatrix.GetLength(0); compass++) 
             {


                blueCompass = 0.0; 
                greenCompass = 0.0; 
                redCompass = 0.0; 


                for (int filterY = -filterOffset; 
                    filterY <= filterOffset; filterY++) 
                 { 
                    for (int filterX = -filterOffset; 
                        filterX <= filterOffset; filterX++) 
                     { 
                        calcOffset = byteOffset + 
                                     (filterX * 4) + 
                                     (filterY * sourceData.Stride); 


                        blueCompass += (double)(pixelBuffer[calcOffset]) * 
                                        filterMatrix[compass, 
                                        filterY + filterOffset, 
                                        filterX + filterOffset]; 


                        greenCompass += (double)(pixelBuffer[calcOffset + 1]) * 
                                        filterMatrix[compass, 
                                        filterY + filterOffset, 
                                        filterX + filterOffset]; 


                        redCompass += (double)(pixelBuffer[calcOffset + 2]) * 
                                        filterMatrix[compass, 
                                        filterY + filterOffset, 
                                        filterX + filterOffset]; 
                     }
                 }


                blue = (blueCompass > blue ? blueCompass : blue); 
                green = (greenCompass > green ? greenCompass : green); 
                red = (redCompass > red ? redCompass : red); 
             }


            blue = factor * blue + bias; 
            green = factor * green + bias; 
            red = factor * red + bias; 


            if(blue > 255) 
             { blue = 255; } 
            else if(blue < 0) 
             { blue = 0; } 


            if(green > 255) 
             { green = 255; } 
            else if(green < 0) 
             { green = 0; } 


            if(red > 255) 
             { red = 255; } 
            else if(red < 0) 
             { red = 0; } 


            resultBuffer[byteOffset] = (byte)(blue); 
            resultBuffer[byteOffset + 1] = (byte)(green); 
            resultBuffer[byteOffset + 2] = (byte)(red); 
            resultBuffer[byteOffset + 3] = 255; 
         }
     } 


    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 


    BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 


    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 


    return resultBitmap; 
}

Rose: Isotropic 3 x 3 x 8

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction. The following image files feature a sample images:

Wasp – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from Wikimedia
Ladybug – Licensed under the Creative Commons Attribution-Share Alike 2.0 Generic license. Download from Wikipedia
Ant – Released into the public domain by its author, Sean.hoyland. This applies worldwide. In some countries this may not be legally possible; if so: Sean.hoyland grants anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law. Download from Wikipedia
Prey Mantis – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from Wikipedia
Bee – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from Wikipedia
Red Pierrot Butterfly 1– Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Download from WikiMedia
Siproeta Epaphus Butterfly – Licensed under the Creative Commons Attribution 3.0 Unported license. Download from WikiMedia
Red Pierrot Butterfly 2 – Licensed under the Creative Commons Attribution 2.0 Generic license. Download from Wikipedia
Iceberg Rose – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Attribution: Stan Shebs. Download from Wikipedia
Heidi Klum Rose – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license. Download from Wikipedia
Viceroy Butterfly – Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Attributed to D. Gordon E. Robertson. Download from Wikipedia

The Original Image

Butterfly: Isotropic 3 x 3 x 4

Butterfly: Isotropic 3 x 3 x 8

Butterfly: Kirsch 3 x 3 x 4

Butterfly: Kirsch 3 x 3 x 8

Butterfly: Prewitt 3 x 3 x 4

Butterfly: Prewitt 3 x 3 x 8

Butterfly: Prewitt 5 x 5 x 4

Butterfly: Scharr 3 x 3 x 4

Butterfly: Scharr 3 x 3 x 8

Butterfly: Scharr 5 x 5 x 4

Butterfly: Sobel 3 x 3 x 4

Butterfly: Sobel 3 x 3 x 8

Butterfly: Sobel 5 x 5 x 4

C# How to: Image Blur

Published June 9, 2013 Augmented Reality , C# , Code Samples , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Image Processing , Learn Everyday , Microsoft , New Version , Opensource , Update 29 Comments
Tags: Augmented Reality, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Box Blur, C#, Calculating Kernels, Code Sample, Converting Images, Convolution matrix, Feature extraction, Gaussian, Gaussian Blur, Gaussian Kernels, Graphic Filters, Image, Image Blur, Image processing, Image Smoothing, Image Transform, Machine vision, Matrix, Mean Filter, Median Filter, Motion Blur, Pixel Filters

Article Purpose

This article serves to provides an introduction and discussion relating to Image Blurring methods and techniques. The Image Blur methods covered in this article include: Box Blur, Gaussian Blur, Mean Filter, Median Filter and Motion Blur.

Daisy: Mean 9×9

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

This article is accompanied by a sample application, intended to provide a means of testing and replicating topics discussed in this article. The sample application is a Windows Forms based application of which the user interface enables the user to select an Image Blur type to implement.

When clicking the Load Image button users are able to browse the local file system in order to select source/input images. In addition users are also able to save blurred result images when clicking the Save Image button and browsing the local file system.

Daisy: Mean 7×7

The sample application provides the user with the ability to select the method of image blurring to implement. The combobox dropdown located on the right-hand side of the user interface lists all of the supported methods of image blurring. When a user selects an item from the combobox, the associated blur method will be implemented on the preview image.

The image below is a screenshot of the Image Blur Filter sample application in action:

Image Blur Overview

The process of image blurring can be regarded as reducing the sharpness or crispness defined by an image. Image blurring results in image detail/definition being perceived as less distinct. Images are often blurred as a method of smoothing an image.

Images perceived as too crisp/sharp can be softened by applying a variety of image blurring techniques and intensity levels. Often images are smoothed/blurred in order to remove/reduce image noise. In image edge detection implementations better results are often achieved when first implementing noise reduction through smoothing/blurring. Image blurring can even be implemented in a fashion where results reflect image edge detection, a method known as Difference of Gaussians.

In this article and the accompanying sample source code all methods of image blurring supported have been implemented through image convolution, with the exception of the Median filter. Each of the supported methods in essence only represent a different convolution matrix kernel. The image blurring technique capable of achieving optimal results will to varying degrees be dependent on the features present in the specified source/input image. Each method provides a different set of desired properties and compromises. In the following sections an overview of each method will be discussed.

Daisy: Mean 9×9

Mean Filter/Box Blur

The Mean Filter also sometimes referred to as a Box Blur represents a fairly simplistic implementation and definition. A Mean Filter definition can be found on Wikipedia as follows:

A box blur is an image filter in which each pixel in the resulting image has a value equal to the average value of its neighbouring pixels in the input image. It is a form of low-pass ("blurring") filter and is a convolution.

Due to its property of using equal weights it can be implemented using a much simpler accumulation algorithm which is significantly faster than using a sliding window algorithm.

Mean Filter as a title relates to all weight values in a convolution kernel being equal, therefore the alternate title of Box Blur. In most cases a Mean Filter matrix kernel will only contain the value one. When performing image convolution implementing a Mean Filter kernel, the factor value equates to the 1 being divided by the sum of all kernel values.

The following is an example of a 5×5 Mean Filter convolution kernel:

The kernel consist of 25 elements, therefore the factor value equates to one divided by twenty five.

The Mean Filter Blur does not result in the same level of smoothing achieved by other image blur methods. The Mean Filter method can also be susceptible to directional artefacts.

Daisy Mean 5×5

Gaussian Blur

The Gaussian method of image blurring is a popular and often implemented filter. In contrast to the Box Blur method Gaussian Blurring produce resulting images appearing to contain a more uniform level of smoothing. When implementing image edge detection a Gaussian Blur is often applied to source/input images resulting in noise reduction. The Gaussian Blur has a good level of image edge preservation, hence being used in edge detection operations.

From Wikipedia we gain the following description:

A Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail. The visual effect of this blurring technique is a smooth blur resembling that of viewing the image through a translucent screen, distinctly different from the bokeh effect produced by an out-of-focus lens or the shadow of an object under usual illumination. Gaussian smoothing is also used as a pre-processing stage in computer vision algorithms in order to enhance image structures at different scales

A potential drawback to implementing a Gaussian blur results from the filter being computationally intensive. The following matrix kernel represents a 5×5 Gaussian Blur. The sum total of all elements in the kernel equate to 159, therefore a factor value of 1.0 / 159.0 will be implemented.

Daisy: Gaussian 5×5

Median Filter Blur

The Median Filter is classified as a non-linear filter. In contrast to the other methods of image blurring discussed in this article the Median Filter implementation does not involve convolution or a predefined matrix kernel. The following description can be found on Wikipedia:

In signal processing, it is often desirable to be able to perform some kind of noise reduction on an image or signal. The median filter is a nonlinear digital filtering technique, often used to remove noise. Such noise reduction is a typical pre-processing step to improve the results of later processing (for example, edge detection on an image). Median filtering is very widely used in digital image processing because, under certain conditions, it preserves edges while removing noise.

Daisy: Median 7×7

As the name implies, the Median Filter operates by calculating the median value of a pixel group also referred to as a window. Calculating a Median value involves a number of steps. The required steps are listed as follows:

Iterate each pixel that forms part of the source/input image.
In relation to the pixel currently being iterated determine neighbouring pixels located within the bounds defined by the window size. The window location should be offset in order to align the window’s middle pixel and the pixel currently being iterated.
Neighbouring pixels located within the bounds defined by the window should be added to a one dimensional neighbourhood array. Once all value have been added, the array should be sorted by value.
The pixel value located at the middle of the sorted neighbourhood array qualifies as the Median value. The newly determined Median value should be assigned to the pixel currently being iterated.
Repeat the steps listed above until all pixels within the source/input image have been iterated.

Similar to the Gaussian Blur filter the Median Filter has the ability to smooth image noise whilst providing edge preservation. Depending on the window size implemented and the physical dimensions of input/source images the Median Filter can be computationally expensive.

Daisy: Median 9×9

Motion Blur

The sample source implements Motion Blur filters. Motion blurring in the traditional sense has been association with photography and video capturing. Motion Blurring can often be observed in scenarios where rapid movements are being captured to photographs or video recording. When recording a single frame, rapid movements could result in the image changing before the frame being captured has completed.

Motion Blurring can be synthetically imitated through the implementation of Digital Motion Blur filters. The size of the matrix kernel provided when implementing image convolution affects the filter intensity perceived in result images. Relating to Motion Blur filters the size of the kernel specified in convolution influences the perception and appearance of how rapidly movement had occurred to have blurred the resulting image. Larger kernels produce the appearance of more rapid motion, whereas smaller kernels result in less rapid motion being perceived.

Daisy: Motion Blur 7×7 135 Degrees

Depending on the kernel specified the ability exists to create the appearance of movement having occurred in a certain direction. The sample source code implements Motion Blur filters at 45 degrees, 135 degrees and in both directions simultaneously.

The kernel listed below represents a 5×5 Motion Blur filter occurring at 45 degrees and 135 degrees:

Image Blur Implementation

The sample source code implements all of the concepts explored throughout this article. The source code definition can be grouped into 4 sections: ImageBlurFilter method, ConvolutionFilter method, MedianFilter method and the Matrix class. The following article sections relate to the 4 main source code sections.

The ImageBlurFilter extension method has the purpose of invoking the correct blur filter method and relevant method parameters. This method acts as a method wrapper providing the technical implementation details required when performing a specified blur filter.

The definition of the ImageBlurFilter extension method as follows:

 public static Bitmap ImageBlurFilter(this Bitmap sourceBitmap,  
                                             BlurType blurType) 
{  
     Bitmap resultBitmap = null; 

       
     switch (blurType) 
     {  
         case BlurType.Mean3x3: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean3x3, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.Mean5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean5x5, 1.0 / 25.0, 0); 
              } break; 
         case BlurType.Mean7x7: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean7x7, 1.0 / 49.0, 0); 
              } break; 
         case BlurType.Mean9x9: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                                Matrix.Mean9x9, 1.0 / 81.0, 0); 
              } break; 
         case BlurType.GaussianBlur3x3: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                         Matrix.GaussianBlur3x3, 1.0 / 16.0, 0); 
              } break; 
         case BlurType.GaussianBlur5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                        Matrix.GaussianBlur5x5, 1.0 / 159.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                           Matrix.MotionBlur5x5, 1.0 / 10.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur5x5At45Degrees, 1.0 / 5.0, 0); 
              } break; 
         case BlurType.MotionBlur5x5At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur5x5At135Degrees, 1.0 / 5.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7, 1.0 / 14.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7At45Degrees, 1.0 / 7.0, 0); 
              } break; 
         case BlurType.MotionBlur7x7At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur7x7At135Degrees, 1.0 / 7.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9, 1.0 / 18.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9At45Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9At45Degrees, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.MotionBlur9x9At135Degrees: 
              {  
                 resultBitmap = sourceBitmap.ConvolutionFilter( 
                 Matrix.MotionBlur9x9At135Degrees, 1.0 / 9.0, 0); 
              } break; 
         case BlurType.Median3x3: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(3); 
              } break; 
         case BlurType.Median5x5: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(5); 
              } break; 
         case BlurType.Median7x7: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(7); 
              } break; 
         case BlurType.Median9x9: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(9); 
              } break; 
         case BlurType.Median11x11: 
              {  
                 resultBitmap = sourceBitmap.MedianFilter(11); 
              } break; 
      }  

   
     return resultBitmap; 
}

Daisy: Motion Blur 9×9

The Matrix class serves as a collection of various kernel definitions. The Matrix class and all public properties are defined as static. The definition of the Matrix class as follows:

     public static class Matrix 
    {  
         public static double[,] Mean3x3 
         {  
             get 
             {  
                 return new double[,]   
                { {  1, 1, 1, },  
                  {  1, 1, 1, },  
                  {  1, 1, 1, }, }; 
             }  
         }  

  
         public static double[,] Mean5x5 
         {  
             get 
             {  
                 return new double[,]   
                { {  1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1 }, }; 
            }  
        }  

    
        public static double[,] Mean7x7 
        {  
             get 
             {  
                return new double[,]   
                { {  1, 1, 1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1 }, }; 
             }  
        }  

    
         public static double[,] Mean9x9 
         {  
             get 
             {  
                return new double[,]   
                { {  1, 1, 1, 1, 1, 1, 1, 1, 1 },  
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, 
                  {  1, 1, 1, 1, 1, 1, 1, 1, 1 }, }; 
            }  
        }  

    
        public static double[,] GaussianBlur3x3 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 2, 1, },  
                  {  2, 4, 2, },  
                  {  1, 2, 1, }, }; 
            }  
        }  

    
        public static double[,] GaussianBlur5x5 
        {  
            get 
            {  
                return new double[,]   
                { {  2, 04, 05, 04, 2 },  
                  {  4, 09, 12, 09, 4 },  
                  {  5, 12, 15, 12, 5 }, 
                  {  4, 09, 12, 09, 4 }, 
                  {  2, 04, 05, 04, 2 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5 
        {  
             get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 1 },  
                  {  0, 1, 0, 1, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 1, 0 }, 
                  {  1, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5At45Degrees 
        {  
             get 
            {  
                return new double[,]   
                { {  0, 0, 0, 0, 1 },  
                  {  0, 0, 0, 1, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 0, 0 }, 
                  {  1, 0, 0, 0, 0 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur5x5At135Degrees 
        {  
             get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0 },  
                  {  0, 1, 0, 0, 0 },  
                  {  0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0 }, 
                  {  0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0, 0, 1 },  
                  {  0, 1, 0, 0, 0, 1, 0 },  
                  {  0, 0, 1, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 1, 0, 1, 0, 0 }, 
                  {  0, 1, 0, 0, 0, 1, 0 }, 
                  {  1, 0, 0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7At45Degrees 
        {  
            get 
            {  
                return new double[,]   
                { {  0, 0, 0, 0, 0, 0, 1 },  
                  {  0, 0, 0, 0, 0, 1, 0 },  
                  {  0, 0, 0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 1, 0, 0, 0, 0 }, 
                  {  0, 1, 0, 0, 0, 0, 0 }, 
                  {  1, 0, 0, 0, 0, 0, 0 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur7x7At135Degrees 
        {  
            get 
            {  
                return new double[,]   
                { {  1, 0, 0, 0, 0, 0, 0 },  
                  {  0, 1, 0, 0, 0, 0, 0 },  
                  {  0, 0, 1, 0, 0, 0, 0 }, 
                  {  0, 0, 0, 1, 0, 0, 0 }, 
                  {  0, 0, 0, 0, 1, 0, 0 }, 
                  {  0, 0, 0, 0, 0, 1, 0 }, 
                  {  0, 0, 0, 0, 0, 0, 1 }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9 
        {  
            get 
            {  
                return new double[,]   
                { { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 1, 0, 0, 0, 0, 0, 0, 0, 1, }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9At45Degrees 
        {  
             get 
            {  
                return new double[,]   
                { { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, }; 
            }  
        }  

    
        public static double[,] MotionBlur9x9At135Degrees 
        {  
             get 
            {  
                return new double[,]   
                { { 1, 0, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 1, 0, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 1, 0, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 1, 0, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 1, 0, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 1, 0, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 1, 0, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 1, 0, }, 
                  { 0, 0, 0, 0, 0, 0, 0, 0, 1, }, }; 
            }  
        }  
    }

Daisy: Median 7×7

The MedianFilter extension method targets the Bitmap class. The MedianFilter method applies a Median Filter using the specified Bitmap and matrix size (window size), returning a new Bitmap representing the filtered image.

The definition of the MedianFilter extension method as follows:

 public static Bitmap MedianFilter(this Bitmap sourceBitmap, 
                                   int matrixSize) 
{ 
     BitmapData sourceData = 
                sourceBitmap.LockBits(new Rectangle(0, 0, 
                sourceBitmap.Width, sourceBitmap.Height), 
                ImageLockMode.ReadOnly, 
                PixelFormat.Format32bppArgb); 

   
     byte[] pixelBuffer = new byte[sourceData.Stride * 
                                   sourceData.Height]; 

   
     byte[] resultBuffer = new byte[sourceData.Stride * 
                                    sourceData.Height]; 

   
     Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, 
                                pixelBuffer.Length); 

   
     sourceBitmap.UnlockBits(sourceData); 

   
     int filterOffset = (matrixSize - 1) / 2; 
     int calcOffset = 0; 

   
     int byteOffset = 0; 

   
     List<int> neighbourPixels = new List<int>(); 
     byte[] middlePixel; 

   
     for (int offsetY = filterOffset; offsetY < 
         sourceBitmap.Height - filterOffset; offsetY++) 
     { 
         for (int offsetX = filterOffset; offsetX < 
             sourceBitmap.Width - filterOffset; offsetX++) 
         { 
             byteOffset = offsetY * 
                          sourceData.Stride + 
                          offsetX * 4; 

   
             neighbourPixels.Clear(); 

   
             for (int filterY = -filterOffset; 
                 filterY <= filterOffset; filterY++) 
             {
                 for (int filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                 {

   
                     calcOffset = byteOffset + 
                                  (filterX * 4) + 
                                  (filterY * sourceData.Stride); 

   
                     neighbourPixels.Add(BitConverter.ToInt32( 
                                      pixelBuffer, calcOffset)); 
                 } 
             } 

   
             neighbourPixels.Sort(); 
  
             middlePixel = BitConverter.GetBytes( 
                                neighbourPixels[filterOffset]); 

   
             resultBuffer[byteOffset] = middlePixel[0]; 
             resultBuffer[byteOffset + 1] = middlePixel[1]; 
             resultBuffer[byteOffset + 2] = middlePixel[2]; 
             resultBuffer[byteOffset + 3] = middlePixel[3]; 
         } 
     }

   
     Bitmap resultBitmap = new Bitmap (sourceBitmap.Width, 
                                      sourceBitmap.Height); 

   
     BitmapData resultData = 
                resultBitmap.LockBits(new Rectangle  (0, 0, 
                resultBitmap.Width, resultBitmap.Height), 
                ImageLockMode.WriteOnly, 
                PixelFormat.Format32bppArgb); 

   
     Marshal.Copy(resultBuffer, 0, resultData.Scan0, 
                                resultBuffer.Length); 

   
     resultBitmap.UnlockBits(resultData); 

   
     return resultBitmap; 
}

Daisy: Motion Blur 9×9

The sample source code performs image convolution by invoking the ConvolutionFilter extension method.

The definition of the ConvolutionFilter extension method as follows:

private static Bitmap ConvolutionFilter(this Bitmap sourceBitmap, 
                                          double[,] filterMatrix, 
                                               double factor = 1, 
                                                    int bias = 0) 
{ 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle(0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

   
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 

   
    double blue = 0.0; 
    double green = 0.0; 
    double red = 0.0; 

   
    int filterWidth = filterMatrix.GetLength(1); 
    int filterHeight = filterMatrix.GetLength(0); 

   
    int filterOffset = (filterWidth - 1) / 2; 
    int calcOffset = 0; 

   
    int byteOffset = 0; 

   
    for (int offsetY = filterOffset; offsetY < 
        sourceBitmap.Height - filterOffset; offsetY++) 
     { 
        for (int offsetX = filterOffset; offsetX < 
            sourceBitmap.Width - filterOffset; offsetX++) 
         { 
            blue = 0; 
            green = 0; 
            red = 0; 

   
            byteOffset = offsetY * 
                         sourceData.Stride + 
                         offsetX * 4; 

   
            for (int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++) 
             { 
                for (int filterX = -filterOffset; 
                    filterX <= filterOffset; filterX++) 
                 { 

   
                    calcOffset = byteOffset + 
                                 (filterX * 4) + 
                                 (filterY * sourceData.Stride); 

   
                    blue += (double)(pixelBuffer[calcOffset]) * 
                            filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    green += (double)(pixelBuffer[calcOffset + 1]) * 
                             filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    red += (double)(pixelBuffer[calcOffset + 2]) * 
                           filterMatrix[filterY + filterOffset, 
                                              filterX + filterOffset]; 
                 } 
             }

   
            blue = factor * blue + bias; 
            green = factor * green + bias; 
            red = factor * red + bias; 

   
            blue = (blue > 255 ? 255 : 
                   (blue < 0 ? 0 : 
                    blue)); 

   
            green = (green > 255 ? 255 : 
                    (green < 0 ? 0 : 
                     green)); 

   
            red = (red > 255 ? 255 : 
                  (red < 0 ? 0 : 
                   red));  

   
            resultBuffer[byteOffset] = (byte)(blue); 
            resultBuffer[byteOffset + 1] = (byte)(green); 
            resultBuffer[byteOffset + 2] = (byte)(red); 
            resultBuffer[byteOffset + 3] = 255; 
         } 
     }

   
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 

   
    BitmapData resultData = resultBitmap.LockBits(new Rectangle (0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

   
    return resultBitmap; 
}

Sample Images

This article features a number of sample images. All featured images have been licensed allowing for reproduction.

The sample images featuring an image of a yellow daisy is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license and can be downloaded from Wikimedia.org.

The sample images featuring an image of a white daisy is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license and can be downloaded from Wikipedia.

The sample images featuring an image of a pink daisy is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license and can be downloaded from Wikipedia.

The sample images featuring an image of a purple daisy is licensed under the Creative Commons Attribution-ShareAlike 3.0 License and can be downloaded from Wikipedia.

The Original Image

Daisy: Gaussian 3×3

Daisy: Gaussian 5×5

Daisy: Mean 3×3

Daisy: Mean 5×5

Daisy: Mean 7×7

Daisy: Mean 9×9

Daisy: Median 3×3

Daisy: Median 5×5

Daisy: Median 7×7

Daisy: Median 9×9

Daisy: Median 11×11

Daisy: Motion Blur 5×5

Daisy: Motion Blur 5×5 45 Degrees

Daisy: Motion Blur 5×5 135 Degrees

Daisy: Motion Blur 7×7

Daisy: Motion Blur 7×7 45 Degrees

Daisy: Motion Blur 7×7 135 Degrees

Daisy: Motion Blur 9×9

Daisy: Motion Blur 9×9 45 Degrees

Daisy: Motion Blur 9×9 135 Degrees

C# How to: Sharpen Edge Detection

Published June 7, 2013 Augmented Reality , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Arithmetic , Image Convolution , Image Filters , Image Processing , Learn Everyday , Microsoft , New Version , Opensource , Tip , Update 30 Comments
Tags: Augmented Reality, Binary Image, Bitmap ARGB, Bitmap Filters, Bitmap.LockBits, BitmapData, Boolean Edge Detection, C#, Change detection, Code Sample, Computer vision, Converting Images, Convolution matrix, Feature extraction, Graphic Filters, Image, Image Edge Detection, Image processing, Image Sharpen, Image Sharpness, Image Transform, Line Detection, Machine vision, Matrix, Pixel Filters

Article Purpose

It is the objective of this article to explore and provide a discussion based in the concept of Edge Detection through means of Image Sharpening. Illustrated are various methods of image sharpening and in addition a Median filter implemented in image noise reduction.

Sample Source Code

This article is accompanied by a sample source code Visual Studio project which is available for download here.

Using the Sample Application

The sample source code accompanying this article includes a Windows Forms based Sample Application. The concepts illustrated throughout this article can easily be tested and replicated by making use of the Sample Application.

The Sample Application exposes seven main areas of functionality:

Loading input/source images.
Saving image result.
Sharpen Filters
Median Filter Size
Threshold value
Grayscale Source
Mono Output

When using the Sample application users are able to select input/source images from the local file system by clicking the Load Image button. If desired, users may save result images to the local file system by clicking the Save Image button.

The sample source code and sample application implement various methods of Image Sharpening. Each method of image sharpening results in varying degrees of image edge detection. Some methods are more effective than other methods. The image sharpening method being implemented serves as a primary factor influencing edge detection results. The effectiveness of the selected image sharpening method is reliant on the input/source image provided. The sample application implements the following image sharpening methods:

Sharpen5To4
Sharpen7To1
Sharpen9To1
Sharpen12To1
Sharpen24To1
Sharpen48To1
Sharpen10To8
Sharpen11To8
Sharpen821

Image noise is regarded as a common problem relating to image edge detection. Often image noise will be incorrectly detected as forming part of an edge within an image. The sample source code implements a Median filter in order to counter act image noise. The size/intensity of the Median filter applied can be specified via the combobox labelled Median Filter Size.

The Threshold value configured through the sample application’s user interface has a two-fold implementation. In a scenario where output images are created in a black and white format the Threshold value will be implemented to determine whether a pixel should be either black or white. When output images are created as full colour images the Threshold value will be added to each pixel, acting as a bias value.

In some scenarios Image Edge Detection can be achieved more effectively when specifying grayscale format source/input images. The purpose of the checkbox labelled Grayscale Source is to format source/input images in a grayscale format before implementing image edge detection.

The checkbox labelled Mono Output, when selected, has the effect of producing result images in a black and white format.

The image below is a screenshot of the Sharpen Edge Detection sample application in action:

Edge Detection through Image Sharpening

The sample source code performs edge detection on source/input images by means of image sharpening. The steps performed can be broken down to the following items:

If specified, apply a Median filter to the input/source image. A Median filter results in smoothing an image. Image noise can be reduced when implementing a Median Filter. Image smoothing/blurring often results reducing image details/definition. The Median Filter is well suited to smoothing away image noise whilst implementing edge preservation. When performing edge detection the Median filter functions as an ideal method of reducing image noise whilst not negatively impacting edge detection tasks.
If specified, convert the source/input image to grayscale by iterating each pixel that forms part of the image. Each pixel’s colour components are calculated multiplying by factor values: Red x 0.3 Green x 0.59 Blue x 0.11.
Using the specified matrix kernel iterate each pixel forming part of the source/input image, performing image convolution on each pixel colour channel.
If the output image has been specified as Mono, the middle pixel calculated in convolution should be multiplied with the specified factor value. Each colour component should be compared to the specified threshold value and be assigned as either black or white.
If the output image has not been specified as Mono, the middle pixel calculated in convolution should be multiplied with the factor value to which the threshold/bias value should be added. The value of each colour component will be set to the result of subtracting the calculated convolution/filter/bias value from the pixel’s original colour component value. In other words perform image sharpening using convolution applying a factor and bias which should then be subtracted from the original source/input image.

Implementing Sharpen Edge Detection

The sample source code achieves edge detection through image sharpening by implementing three methods: MedianFilter and two overloaded methods titled SharpenEdgeDetect.

The MedianFilter method is defined as an extension method targeting the Bitmap class. The definition as follows:

 public static Bitmap MedianFilter(this Bitmap sourceBitmap, 
                                   int matrixSize) 
{ 
     BitmapData sourceData = 
                sourceBitmap.LockBits(new Rectangle(0, 0, 
                sourceBitmap.Width, sourceBitmap.Height), 
                ImageLockMode.ReadOnly, 
                PixelFormat.Format32bppArgb); 

   
     byte[] pixelBuffer = new byte[sourceData.Stride * 
                                   sourceData.Height]; 

   
     byte[] resultBuffer = new byte[sourceData.Stride * 
                                    sourceData.Height]; 

   
     Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, 
                                pixelBuffer.Length); 

   
     sourceBitmap.UnlockBits(sourceData); 

   
     int filterOffset = (matrixSize - 1) / 2; 
     int calcOffset = 0; 

   
     int byteOffset = 0; 

   
     List<int> neighbourPixels = new List<int>(); 
     byte[] middlePixel; 

   
     for (int offsetY = filterOffset; offsetY < 
         sourceBitmap.Height - filterOffset; offsetY++) 
     { 
         for (int offsetX = filterOffset; offsetX < 
             sourceBitmap.Width - filterOffset; offsetX++) 
         { 
             byteOffset = offsetY * 
                          sourceData.Stride + 
                          offsetX * 4; 

   
             neighbourPixels.Clear(); 

   
             for (int filterY = -filterOffset; 
                 filterY <= filterOffset; filterY++) 
             {
                 for (int filterX = -filterOffset; 
                     filterX <= filterOffset; filterX++) 
                 {

   
                     calcOffset = byteOffset + 
                                  (filterX * 4) + 
                                  (filterY * sourceData.Stride); 

   
                     neighbourPixels.Add(BitConverter.ToInt32( 
                                      pixelBuffer, calcOffset)); 
                 } 
             } 

   
             neighbourPixels.Sort(); 
  
             middlePixel = BitConverter.GetBytes( 
                                neighbourPixels[filterOffset]); 

   
             resultBuffer[byteOffset] = middlePixel[0]; 
             resultBuffer[byteOffset + 1] = middlePixel[1]; 
             resultBuffer[byteOffset + 2] = middlePixel[2]; 
             resultBuffer[byteOffset + 3] = middlePixel[3]; 
         } 
     }

   
     Bitmap resultBitmap = new Bitmap (sourceBitmap.Width, 
                                      sourceBitmap.Height); 

   
     BitmapData resultData = 
                resultBitmap.LockBits(new Rectangle  (0, 0, 
                resultBitmap.Width, resultBitmap.Height), 
                ImageLockMode.WriteOnly, 
                PixelFormat.Format32bppArgb); 

   
     Marshal.Copy(resultBuffer, 0, resultData.Scan0, 
                                resultBuffer.Length); 

   
     resultBitmap.UnlockBits(resultData); 

   
     return resultBitmap; 
}

The public implementation of the SharpenEdgeDetect extension method has the purpose of translating user specified options into the relevant method calls to the private implementation of the SharpenEdgeDetect extension method. The public implementation of the SharpenEdgeDetect method as follows:

public static Bitmap SharpenEdgeDetect(this Bitmap sourceBitmap, 
                                            SharpenType sharpen, 
                                                   int bias = 0, 
                                         bool grayscale = false, 
                                              bool mono = false, 
                                       int medianFilterSize = 0) 
{ 
    Bitmap resultBitmap = null; 

   
    if (medianFilterSize == 0) 
    {
        resultBitmap = sourceBitmap; 
    } 
    else 
    {
        resultBitmap =  
        sourceBitmap.MedianFilter(medianFilterSize); 
    } 

       
    switch (sharpen) 
    { 
        case SharpenType.Sharpen7To1: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                             Matrix.Sharpen7To1,  
                             1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen9To1: 
            { 
                resultBitmap =  
                    resultBitmap.SharpenEdgeDetect( 
                                Matrix.Sharpen9To1,  
                                1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen12To1: 
            { 
                resultBitmap =  
                    resultBitmap.SharpenEdgeDetect( 
                                Matrix.Sharpen12To1,  
                                1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen24To1: 
            {
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen24To1,  
                            1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen48To1: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen48To1,  
                            1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen5To4: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen5To4,  
                            1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen10To8: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen10To8,  
                            1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen11To8: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen11To8,  
                            3.0 / 1.0, bias, grayscale, mono); 
            } break; 
        case SharpenType.Sharpen821: 
            { 
                resultBitmap =  
                resultBitmap.SharpenEdgeDetect( 
                            Matrix.Sharpen821,  
                            8.0 / 1.0, bias, grayscale, mono); 
            } break; 
    } 

   
    return resultBitmap; 
}

The Matrix class provides the definition of static pre-defined matrix kernel values. The definition as follows:

public static class Matrix   
{
    public static double[,] Sharpen7To1 
    {
        get   
        { 
            return new double[,]   
            {  { 1,  1,  1, },  
               { 1, -7,  1, },   
               { 1,  1,  1, }, }; 
        }  
    }  

   
    public static double[,] Sharpen9To1 
    {  
        get   
        {  
            return new double[,]   
            {  { -1, -1, -1, },  
               { -1,  9, -1, },   
               { -1, -1, -1, }, }; 
        }  
    }  

   
    public static double[,] Sharpen12To1 
    {  
        get   
        {  
            return new double[,]   
            {  { -1, -1, -1, },  
               { -1, 12, -1, },   
               { -1, -1, -1, }, }; 
        }  
    }  

   
    public static double[,] Sharpen24To1 
    {  
        get   
        {  
            return new double[,]   
            {  { -1, -1, -1, -1, -1, },  
               { -1, -1, -1, -1, -1, },  
               { -1, -1, 24, -1, -1, },  
               { -1, -1, -1, -1, -1, },  
               { -1, -1, -1, -1, -1, }, }; 
        }  
    }  

   
    public static double[,] Sharpen48To1 
    {  
        get   
        {  
            return new double[,]   
            {  {  -1, -1, -1, -1, -1, -1, -1, },  
               {  -1, -1, -1, -1, -1, -1, -1, },  
               {  -1, -1, -1, -1, -1, -1, -1, },  
               {  -1, -1, -1, 48, -1, -1, -1, },  
               {  -1, -1, -1, -1, -1, -1, -1, },  
               {  -1, -1, -1, -1, -1, -1, -1, },  
               {  -1, -1, -1, -1, -1, -1, -1, }, }; 
        }  
    }  

   
    public static double[,] Sharpen5To4 
    {  
        get   
        {  
            return new double[,]  
            {  {  0, -1,  0, },  
               { -1,  5, -1, },  
               {  0, -1,  0, }, }; 
        }  
    }  

   
    public static double[,] Sharpen10To8 
    {  
        get   
        {  
            return new double[,]  
            {  {  0, -2,  0, },  
               { -2, 10, -2, },  
               {  0, -2,  0, }, }; 
        }  
    }  

   
    public static double[,] Sharpen11To8 
    {  
        get   
        {  
            return new double[,]   
            {  {  0, -2,  0, },  
               { -2, 11, -2, },  
               {  0, -2,  0, }, }; 
        }  
    }  

   
    public static double[,] Sharpen821 
    {  
        get   
        {  
            return new double[,]   
            {  {  -1, -1, -1, -1, -1, },  
               {  -1,  2,  2,  2, -1, },  
               {  -1,  2,  8,  2,  1, }, 
               {  -1,  2,  2,  2, -1, }, 
               {  -1, -1, -1, -1, -1, }, }; 
        }  
    }  
}

The private implementation of the SharpenEdgeDetect extension method performs image sharpening through convolution and then performs image subtraction. The definition as follows:

private static Bitmap SharpenEdgeDetect(this Bitmap sourceBitmap, 
                                          double[,] filterMatrix, 
                                               double factor = 1, 
                                                    int bias = 0, 
                                          bool grayscale = false, 
                                               bool mono = false) 
{ 
    BitmapData sourceData = sourceBitmap.LockBits(new Rectangle(0, 0, 
                             sourceBitmap.Width, sourceBitmap.Height), 
                                               ImageLockMode.ReadOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    byte[] pixelBuffer = new byte[sourceData.Stride * sourceData.Height]; 
    byte[] resultBuffer = new byte[sourceData.Stride * sourceData.Height]; 

   
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0, pixelBuffer.Length); 
    sourceBitmap.UnlockBits(sourceData); 

   
    if (grayscale == true) 
    { 
        for (int pixel = 0; pixel < pixelBuffer.Length; pixel += 4) 
        { 
            pixelBuffer[pixel] =  
                (byte)(pixelBuffer[pixel] * 0.11f); 

   
            pixelBuffer[pixel + 1] =  
                (byte)(pixelBuffer[pixel + 1] * 0.59f); 

   
            pixelBuffer[pixel + 2] =  
                (byte)(pixelBuffer[pixel + 2] * 0.3f); 
        } 
    }

   
    double blue = 0.0; 
    double green = 0.0; 
    double red = 0.0; 

   
    int filterWidth = filterMatrix.GetLength(1); 
    int filterHeight = filterMatrix.GetLength(0); 

   
    int filterOffset = (filterWidth - 1) / 2; 
    int calcOffset = 0; 

   
    int byteOffset = 0; 

   
    for (int offsetY = filterOffset; offsetY < 
        sourceBitmap.Height - filterOffset; offsetY++) 
    { 
        for (int offsetX = filterOffset; offsetX < 
            sourceBitmap.Width - filterOffset; offsetX++) 
        {
            blue = 0; 
            green = 0; 
            red = 0; 

   
            byteOffset = offsetY * 
                         sourceData.Stride + 
                         offsetX * 4; 

   
            for (int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++) 
            {
                for (int filterX = -filterOffset; 
                    filterX <= filterOffset; filterX++) 
                {
                    calcOffset = byteOffset + 
                                 (filterX * 4) + 
                                 (filterY * sourceData.Stride); 

   
                    blue += (double  )(pixelBuffer[calcOffset]) * 
                            filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    green += (double  )(pixelBuffer[calcOffset + 1]) * 
                             filterMatrix[filterY + filterOffset, 
                                                filterX + filterOffset]; 

   
                    red += (double  )(pixelBuffer[calcOffset + 2]) * 
                           filterMatrix[filterY + filterOffset, 
                                              filterX + filterOffset]; 
                }
            }

   
            if (mono == true) 
            { 
                blue = resultBuffer[byteOffset] - factor * blue; 
                green = resultBuffer[byteOffset + 1] - factor * green; 
                red = resultBuffer[byteOffset + 2] - factor * red; 

   
                blue = (blue > bias ? 255 : 0); 

   
                green = (blue > bias ? 255 : 0); 

   
                red = (blue > bias ? 255 : 0); 
            }
            else 
            {
                blue = resultBuffer[byteOffset] -  
                       factor * blue + bias; 

   
                green = resultBuffer[byteOffset + 1] -  
                        factor * green + bias; 

   
                red = resultBuffer[byteOffset + 2] -  
                      factor * red + bias; 

   
                blue = (blue > 255 ? 255 : 
                       (blue < 0 ? 0 : 
                        blue)); 

   
                green = (green > 255 ? 255 : 
                        (green < 0 ? 0 : 
                         green)); 

   
                red = (red > 255 ? 255 : 
                      (red < 0 ? 0 : 
                       red)); 
            }  

   
            resultBuffer[byteOffset] = (byte)(blue); 
            resultBuffer[byteOffset + 1] = (byte)(green); 
            resultBuffer[byteOffset + 2] = (byte)(red); 
            resultBuffer[byteOffset + 3] = 255; 
        }
    }

   
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, sourceBitmap.Height); 
 
    BitmapData resultData = resultBitmap.LockBits(new Rectangle(0, 0, 
                             resultBitmap.Width, resultBitmap.Height), 
                                              ImageLockMode.WriteOnly, 
                                         PixelFormat.Format32bppArgb); 

   
    Marshal.Copy(resultBuffer, 0, resultData.Scan0, resultBuffer.Length); 
    resultBitmap.UnlockBits(resultData); 

   
    return resultBitmap; 
}

Sample Images

The sample image used in this article is in the public domain because its copyright has expired. This applies to Australia, the European Union and those countries with a copyright term of life of the author plus 70 years. The original image can be downloaded from Wikipedia.

The Original Image