« C# How to: Image Convolution
C# How to: Difference Of Gaussians »

C# How to: Image Edge Detection

Published May 11, 2013 Augmented Reality , C# , Code Samples , Edge Detection , Extension Methods , Graphic Filters , Graphics , How to , Image Convolution , Image Filters , Microsoft , Opensource , Wikipedia 32 Comments
Tags: , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

Article Purpose

The objective of this article is to explore various algorithms. The types of discussed are: , , , and . All instances are implemented by means of .

Sample source code

This article is accompanied by a sample source code Visual Studio project which is available for download .

Using the Sample Application

The concepts explored in this article can be easily replicated by making use of the Sample Application, which forms part of the associated sample source code accompanying this article.

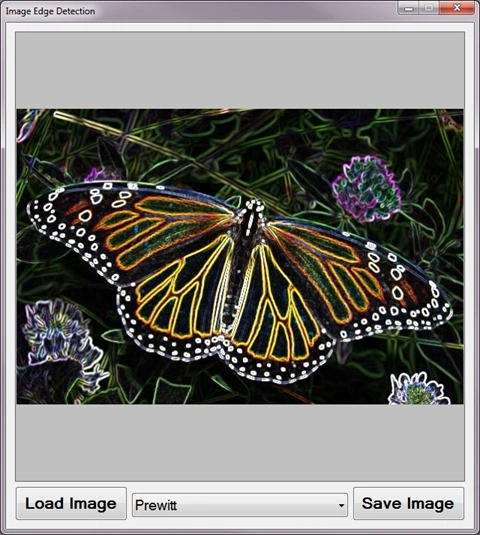
When using the Image Edge Detection sample application you can specify a input/source image by clicking the Load Image button. The dropdown towards the bottom middle part of the screen relates the various methods discussed.

If desired a user can save the resulting image to the local file system by clicking the Save Image button.

The following image is screenshot of the Image Edge Detection sample application in action:

Image Edge Detection Sample Application

Edge Detection

A good description of edge detection forms part of the on :

Edge detection is the name for a set of mathematical methods which aim at identifying points in a at which the changes sharply or, more formally, has discontinuities. The points at which image brightness changes sharply are typically organized into a set of curved line segments termed edges. The same problem of finding discontinuities in 1D signals is known as and the problem of finding signal discontinuities over time is known as . Edge detection is a fundamental tool in , and , particularly in the areas of and .

Image Convolution

A good introduction article  to can be found at: http://homepages.inf.ed.ac.uk/rbf/HIPR2/convolve.htm. From the article we learn the following:

Convolution is a simple mathematical operation which is fundamental to many common image processing operators. Convolution provides a way of `multiplying together’ two arrays of numbers, generally of different sizes, but of the same dimensionality, to produce a third array of numbers of the same dimensionality. This can be used in image processing to implement operators whose output pixel values are simple linear combinations of certain input pixel values.

In an image processing context, one of the input arrays is normally just a graylevel image. The second array is usually much smaller, and is also two-dimensional (although it may be just a single pixel thick), and is known as the kernel.

Single Matrix Convolution

The sample source code implements the ConvolutionFilter method, an targeting the class. The ConvolutionFilter method is intended to apply a user defined and optionally covert an to grayscale. The implementation as follows:

private static Bitmap ConvolutionFilter(Bitmap sourceBitmap, 
                                     double[,] filterMatrix, 
                                          double factor = 1, 
                                               int bias = 0, 
                                     bool grayscale = false) 
{
    BitmapData sourceData = 
                   sourceBitmap.LockBits(new Rectangle(0, 0,
                   sourceBitmap.Width, sourceBitmap.Height),
                                     ImageLockMode.ReadOnly, 
                                PixelFormat.Format32bppArgb);

  
    byte[] pixelBuffer = new byte[sourceData.Stride *
                                  sourceData.Height];

 
    byte[] resultBuffer = new byte[sourceData.Stride *
                                   sourceData.Height];

  
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,
                               pixelBuffer.Length);

 
    sourceBitmap.UnlockBits(sourceData);

  
    if(grayscale == true)
    {
        float rgb = 0;

  
        for(int k = 0; k < pixelBuffer.Length; k += 4)
        {
            rgb = pixelBuffer[k] * 0.11f;
            rgb += pixelBuffer[k + 1] * 0.59f;
            rgb += pixelBuffer[k + 2] * 0.3f;

  
            pixelBuffer[k] = (byte)rgb;
            pixelBuffer[k + 1] = pixelBuffer[k];
            pixelBuffer[k + 2] = pixelBuffer[k];
            pixelBuffer[k + 3] = 255;
        }
    }

  
    double blue = 0.0;
    double green = 0.0;
    double red = 0.0;

  
    int filterWidth = filterMatrix.GetLength(1);
    int filterHeight = filterMatrix.GetLength(0);

  
    int filterOffset = (filterWidth-1) / 2;
    int calcOffset = 0;

  
    int byteOffset = 0;

  
    for(int offsetY = filterOffset; offsetY < 
        sourceBitmap.Height - filterOffset; offsetY++)
    {
        for(int offsetX = filterOffset; offsetX < 
            sourceBitmap.Width - filterOffset; offsetX++)
        {
            blue = 0;
            green = 0;
            red = 0;

  
            byteOffset = offsetY * 
                         sourceData.Stride + 
                         offsetX * 4;

  
            for(int filterY = -filterOffset; 
                filterY <= filterOffset; filterY++)
            {
                for(int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
               {

  
                   calcOffset = byteOffset + 
                                (filterX * 4) + 
                                (filterY * sourceData.Stride);

  
                   blue += (double)(pixelBuffer[calcOffset]) *
                           filterMatrix[filterY + filterOffset, 
                                        filterX + filterOffset];

  
                   green += (double)(pixelBuffer[calcOffset+1]) *
                            filterMatrix[filterY + filterOffset, 
                                         filterX + filterOffset];

  
                   red += (double)(pixelBuffer[calcOffset+2]) *
                          filterMatrix[filterY + filterOffset, 
                                       filterX + filterOffset];
                }
            }

  
            blue = factor * blue + bias;
            green = factor * green + bias;
            red = factor * red + bias;

  
            if(blue > 255)
            { blue = 255;}
            else if(blue < 0)
            { blue = 0;}

  
            if(green > 255)
            { green = 255;}
            else if(green < 0)
            { green = 0;}

  
            if(red > 255)
            { red = 255;}
            else if(red < 0)
            { red = 0;}

  
            resultBuffer[byteOffset] = (byte)(blue);
            resultBuffer[byteOffset + 1] = (byte)(green);
            resultBuffer[byteOffset + 2] = (byte)(red);
            resultBuffer[byteOffset + 3] = 255;
        }
    }

  
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width, 
                                    sourceBitmap.Height);

  
    BitmapData resultData =
               resultBitmap.LockBits(new Rectangle(0, 0,
               resultBitmap.Width, resultBitmap.Height),
                                ImageLockMode.WriteOnly,
                            PixelFormat.Format32bppArgb);

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);
    resultBitmap.UnlockBits(resultData);

  
    return resultBitmap;
}

Horizontal and Vertical Matrix Convolution

The ConvolutionFilter has been overloaded to accept two matrices, representing a vertical and a horizontal . The implementation as follows:

public static Bitmap ConvolutionFilter(this Bitmap sourceBitmap,
                                        double[,] xFilterMatrix,
                                        double[,] yFilterMatrix,
                                              double factor = 1,
                                                   int bias = 0,
                                         bool grayscale = false)
{
    BitmapData sourceData = 
                   sourceBitmap.LockBits(new Rectangle(0, 0,
                   sourceBitmap.Width, sourceBitmap.Height),
                                     ImageLockMode.ReadOnly,
                                PixelFormat.Format32bppArgb);

  
    byte[] pixelBuffer = new byte[sourceData.Stride * 
                                  sourceData.Height];

  
    byte[] resultBuffer = new byte[sourceData.Stride *
                                   sourceData.Height];

  
    Marshal.Copy(sourceData.Scan0, pixelBuffer, 0,
                               pixelBuffer.Length);

  
    sourceBitmap.UnlockBits(sourceData);

  
    if (grayscale == true)
    {
        float rgb = 0;

  
        for (int k = 0; k < pixelBuffer.Length; k += 4)
        {
            rgb = pixelBuffer[k] * 0.11f;
            rgb += pixelBuffer[k + 1] * 0.59f;
            rgb += pixelBuffer[k + 2] * 0.3f;

  
            pixelBuffer[k] = (byte)rgb;
            pixelBuffer[k + 1] = pixelBuffer[k];
            pixelBuffer[k + 2] = pixelBuffer[k];
            pixelBuffer[k + 3] = 255;
        }
    }

  
    double blueX = 0.0;
    double greenX = 0.0;
    double redX = 0.0;

  
    double blueY = 0.0;
    double greenY = 0.0;
    double redY = 0.0;

  
    double blueTotal = 0.0;
    double greenTotal = 0.0;
    double redTotal = 0.0;

  
    int filterOffset = 1;
    int calcOffset = 0;

  
    int byteOffset = 0;

  
    for (int offsetY = filterOffset; offsetY <
        sourceBitmap.Height - filterOffset; offsetY++)
    {
        for (int offsetX = filterOffset; offsetX <
            sourceBitmap.Width - filterOffset; offsetX++)
        {
            blueX = greenX = redX = 0;
            blueY = greenY = redY = 0;

  
            blueTotal = greenTotal = redTotal = 0.0;

  
            byteOffset = offsetY *
                         sourceData.Stride +
                         offsetX * 4;

  
            for (int filterY = -filterOffset;
                filterY <= filterOffset; filterY++)
            {
                for (int filterX = -filterOffset;
                    filterX <= filterOffset; filterX++)
                {
                    calcOffset = byteOffset +
                                 (filterX * 4) +
                                 (filterY * sourceData.Stride);

  
                    blueX += (double)
                              (pixelBuffer[calcOffset]) *
                              xFilterMatrix[filterY + 
                                            filterOffset,
                                            filterX + 
                                            filterOffset];

  
                    greenX += (double)
                          (pixelBuffer[calcOffset + 1]) *
                              xFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    redX += (double)
                          (pixelBuffer[calcOffset + 2]) *
                              xFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    blueY += (double)
                              (pixelBuffer[calcOffset]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    greenY += (double)
                          (pixelBuffer[calcOffset + 1]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];

  
                    redY += (double)
                          (pixelBuffer[calcOffset + 2]) *
                              yFilterMatrix[filterY +
                                            filterOffset,
                                            filterX +
                                            filterOffset];
                }
            }

  
            blueTotal = Math.Sqrt((blueX * blueX) +
                                  (blueY * blueY));

  
            greenTotal = Math.Sqrt((greenX * greenX) +
                                   (greenY * greenY));

  
            redTotal = Math.Sqrt((redX * redX) +
                                 (redY * redY));

  
            if (blueTotal > 255)
            { blueTotal = 255; }
            else if (blueTotal < 0)
            { blueTotal = 0; }

  
            if (greenTotal > 255)
            { greenTotal = 255; }
            else if (greenTotal < 0)
            { greenTotal = 0; }

  
            if (redTotal > 255)
            { redTotal = 255; }
            else if (redTotal < 0)
            { redTotal = 0; }

  
            resultBuffer[byteOffset] = (byte)(blueTotal);
            resultBuffer[byteOffset + 1] = (byte)(greenTotal);
            resultBuffer[byteOffset + 2] = (byte)(redTotal);
            resultBuffer[byteOffset + 3] = 255;
        }
    }

  
    Bitmap resultBitmap = new Bitmap(sourceBitmap.Width,
                                     sourceBitmap.Height);

  
    BitmapData resultData =
               resultBitmap.LockBits(new Rectangle(0, 0,
               resultBitmap.Width, resultBitmap.Height),
                                ImageLockMode.WriteOnly,
                            PixelFormat.Format32bppArgb);

  
    Marshal.Copy(resultBuffer, 0, resultData.Scan0,
                               resultBuffer.Length);
    resultBitmap.UnlockBits(resultData);

  
    return resultBitmap;
}

Original Sample Image

The original source image used to create all of the sample images in this article has been licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license. The original image is attributed to Kenneth Dwain Harrelson and can be downloaded from Wikipedia.

Monarch_In_May

Laplacian Edge Detection

The method of counts as one of the commonly used implementations. From we gain the following definition:

Discrete Laplace operator is often used in image processing e.g. in edge detection and motion estimation applications. The discrete Laplacian is defined as the sum of the second derivatives and calculated as sum of differences over the nearest neighbours of the central pixel.

A number of / variations may be applied with results ranging from slight to fairly pronounced. In the following sections of this article we explore two common implementations, 3×3 and 5×5.

Laplacian 3×3

When implementing a 3×3 you will notice little difference between colour and grayscale result .

public static Bitmap 
Laplacian3x3Filter(this Bitmap sourceBitmap, 
                      bool grayscale = true)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                Matrix.Laplacian3x3,
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}
public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
}

Laplacian 3×3

Laplacian 3x3

Laplacian 3×3 Grayscale

Laplacian 3x3 Grayscale

Laplacian 5×5

The 5×5  produces result with a noticeable difference between colour and grayscale . The detected edges are expressed in a fair amount of fine detail, although the has a tendency to be sensitive to .

public static Bitmap 
Laplacian5x5Filter(this Bitmap sourceBitmap, 
                      bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                Matrix.Laplacian5x5,
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}
public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}

Laplacian 5×5

Laplacian 5x5

Laplacian 5×5 Grayscale

Laplacian 5x5 Grayscale

Laplacian of Gaussian

The (LoG) is a common variation of the filter. is intended to counter the noise sensitivity of the regular filter.

attempts to remove noise by implementing smoothing by means of a . In order to optimize performance we can calculate a single representing a and .

public static Bitmap 
LaplacianOfGaussian(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                         Matrix.LaplacianOfGaussian, 
                                       1.0, 0, true);

 
    return resultBitmap;
}
public static double[,] LaplacianOfGaussian
{ 
    get   
    { 
        return new double[,]
        { {  0,  0, -1,  0,  0 },  
          {  0, -1, -2, -1,  0 },  
          { -1, -2, 16, -2, -1 }, 
          {  0, -1, -2, -1,  0 }, 
          {  0,  0, -1,  0,  0 } };
    } 
}

Laplacian of Gaussian

Laplacian Of Gaussian

Laplacian (3×3) of Gaussian (3×3)

Different variations can be combined in an attempt to produce results best suited to the input . In this case we first apply a 3×3 followed by a 3×3 filter.

public static Bitmap 
Laplacian3x3OfGaussian3x3Filter(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                 Matrix.Gaussian3x3,
                                1.0 / 16.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
} 
public static double[,] Gaussian3x3
{ 
   get   
   { 
       return new double[,]
       { { 1, 2, 1, },  
         { 2, 4, 2, },  
         { 1, 2, 1, } }; 
   } 
}

Laplacian 3×3 Of Gaussian 3×3

Laplacian 3x3 Of Gaussian 3x3

Laplacian (3×3) of Gaussian (5×5 – Type 1)

In this scenario we apply a variation of a 5×5 followed by a 3×3 filter.

public static Bitmap 
Laplacian3x3OfGaussian5x5Filter1(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type1,
                               1.0 / 159.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
} 
public static double[,] Gaussian5x5Type1 
{ 
   get   
   { 
       return new double[,]   
       { { 2, 04, 05, 04, 2 },  
         { 4, 09, 12, 09, 4 },  
         { 5, 12, 15, 12, 5 }, 
         { 4, 09, 12, 09, 4 }, 
         { 2, 04, 05, 04, 2 }, }; 
   } 
}

Laplacian 3×3 Of Gaussian 5×5 – Type 1

Laplacian 3x3 Of Gaussian 5x5 Type1

Laplacian (3×3) of Gaussian (5×5 – Type 2)

The following implementation is very similar to the previous implementation. Applying a variation of a 5×5 results in slight differences.

public static Bitmap 
Laplacian3x3OfGaussian5x5Filter2(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type2,
                               1.0 / 256.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap, 
                         Matrix.Laplacian3x3, 1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian3x3
{ 
   get   
   { 
       return new double[,]
       { { -1, -1, -1, },  
         { -1,  8, -1, },  
         { -1, -1, -1, }, }; 
   } 
} 
public static double[,] Gaussian5x5Type2 
{ 
   get   
   {
       return new double[,]  
       { {  1,   4,  6,  4,  1 },  
         {  4,  16, 24, 16,  4 },  
         {  6,  24, 36, 24,  6 }, 
         {  4,  16, 24, 16,  4 }, 
         {  1,   4,  6,  4,  1 }, }; 
   }
}

Laplacian 3×3 Of Gaussian 5×5 – Type 2

Laplacian 3x3 Of Gaussian 5x5 Type2

Laplacian (5×5) of Gaussian (3×3)

This variation of the filter implements a 3×3 , followed by a 5×5 . The resulting appears significantly brighter when compared to a 3×3 .

public static Bitmap 
Laplacian5x5OfGaussian3x3Filter(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                                 Matrix.Gaussian3x3,
                                1.0 / 16.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap,
                         Matrix.Laplacian5x5, 1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}
public static double[,] Gaussian3x3
{ 
   get   
   { 
       return new double[,]
       { { 1, 2, 1, },  
         { 2, 4, 2, },  
         { 1, 2, 1, } }; 
   } 
}

Laplacian 5×5 Of Gaussian 3×3

Laplacian 5x5 Of Gaussian 3x3

Laplacian (5×5) of Gaussian (5×5 – Type 1)

Implementing a larger results in a higher degree of smoothing, equating to less .

public static Bitmap 
Laplacian5x5OfGaussian5x5Filter1(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type1,
                               1.0 / 159.0, 0, true);

 
    resultBitmap = ExtBitmap.ConvolutionFilter(resultBitmap,
                         Matrix.Laplacian5x5, 1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}
public static double[,] Gaussian5x5Type1 
{ 
   get   
   { 
       return new double[,]   
       { { 2, 04, 05, 04, 2 },  
         { 4, 09, 12, 09, 4 },  
         { 5, 12, 15, 12, 5 }, 
         { 4, 09, 12, 09, 4 }, 
         { 2, 04, 05, 04, 2 }, }; 
   } 
}

Laplacian 5×5 Of Gaussian 5×5 – Type 1

Laplacian 5x5 Of Gaussian 5x5 Type1

Laplacian (5×5) of Gaussian (5×5 – Type 2)

The variation of most applicable when implementing a filter depends on expressed by a source . In this scenario the first variations (Type 1) appears to result in less .

public static Bitmap 
Laplacian5x5OfGaussian5x5Filter2(this Bitmap sourceBitmap)
{
    Bitmap resultBitmap = 
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                            Matrix.Gaussian5x5Type2, 
                               1.0 / 256.0, 0, true);

 
    resultBitmap = 
           ExtBitmap.ConvolutionFilter(resultBitmap, 
                                Matrix.Laplacian5x5, 
                                      1.0, 0, false);

 
    return resultBitmap;
}
public static double[,] Laplacian5x5 
{ 
    get   
    { 
       return new double[,]
       { { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, 24, -1, -1, },  
         { -1, -1, -1, -1, -1, },  
         { -1, -1, -1, -1, -1  } }; 
    } 
}
public static double[,] Gaussian5x5Type2 
{ 
   get   
   {
       return new double[,]  
       { {  1,   4,  6,  4,  1 },  
         {  4,  16, 24, 16,  4 },  
         {  6,  24, 36, 24,  6 }, 
         {  4,  16, 24, 16,  4 }, 
         {  1,   4,  6,  4,  1 }, }; 
   }
}

Laplacian 5×5 Of Gaussian 5×5 – Type 2

Laplacian 5x5 Of Gaussian 5x5 Type2

Sobel Edge Detection

is another common implementation of . We gain the following from :

The Sobel operator is used in , particularly within edge detection algorithms. Technically, it is a , computing an approximation of the of the image intensity function. At each point in the image, the result of the Sobel operator is either the corresponding gradient vector or the norm of this vector. The Sobel operator is based on convolving the image with a small, separable, and integer valued filter in horizontal and vertical direction and is therefore relatively inexpensive in terms of computations. On the other hand, the gradient approximation that it produces is relatively crude, in particular for high frequency variations in the image.

Unlike the filters discussed earlier, filter results differ significantly when comparing colour and grayscale . The filter tends to be less sensitive to compared to the filter. The detected edge lines are not as finely detailed/granular as the detected edge lines resulting from filters.

public static Bitmap 
Sobel3x3Filter(this Bitmap sourceBitmap, 
                  bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                          Matrix.Sobel3x3Horizontal, 
                            Matrix.Sobel3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}
 
public static double[,] Sobel3x3Horizontal
{ 
   get   
   {
       return new double[,]  
       { { -1,  0,  1, },  
         { -2,  0,  2, },  
         { -1,  0,  1, }, }; 
   } 
} 
public static double[,] Sobel3x3Vertical 
{ 
   get   
   { 
       return new double[,]  
       { {  1,  2,  1, },  
         {  0,  0,  0, },  
         { -1, -2, -1, }, }; 
   } 
}

Sobel 3×3

Sobel 3x3

Sobel 3×3 Grayscale

Sobel 3x3 Grayscale

Prewitt Edge Detection

As with the other methods of discussed in this article the method is also a fairly common implementation. From we gain the following quote:

The Prewitt operator is used in , particularly within algorithms. Technically, it is a , computing an approximation of the of the image intensity function. At each point in the image, the result of the Prewitt operator is either the corresponding gradient vector or the norm of this vector. The Prewitt operator is based on convolving the image with a small, separable, and integer valued filter in horizontal and vertical direction and is therefore relatively inexpensive in terms of computations. On the other hand, the gradient approximation which it produces is relatively crude, in particular for high frequency variations in the image. The Prewitt operator was developed by Judith M. S. Prewitt.

In simple terms, the operator calculates the of the image intensity at each point, giving the direction of the largest possible increase from light to dark and the rate of change in that direction. The result therefore shows how "abruptly" or "smoothly" the image changes at that point, and therefore how likely it is that that part of the image represents an edge, as well as how that edge is likely to be oriented. In practice, the magnitude (likelihood of an edge) calculation is more reliable and easier to interpret than the direction calculation.

Similar to the filter, resulting express a significant difference when comparing colour and grayscale .

public static Bitmap 
PrewittFilter(this Bitmap sourceBitmap, 
                 bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                        Matrix.Prewitt3x3Horizontal, 
                          Matrix.Prewitt3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}
public static double[,] Prewitt3x3Horizontal 
{ 
   get   
   { 
       return new double[,]  
       { { -1,  0,  1, },  
         { -1,  0,  1, },  
         { -1,  0,  1, }, }; 
   } 
} 
  
public static double[,] Prewitt3x3Vertical 
{ 
   get   
   { 
       return new double[,]  
       { {  1,  1,  1, },  
         {  0,  0,  0, },  
         { -1, -1, -1, }, }; 
   }
}

Prewitt

Prewitt

Prewitt Grayscale

Prewitt Grayscale

Kirsch Edge Detection

The method is often implemented in the form of Compass . In the following scenario we only implement two components: Horizontal and Vertical. Resulting tend to have a high level of brightness.

public static Bitmap 
KirschFilter(this Bitmap sourceBitmap, 
                bool grayscale = true)
{
    Bitmap resultBitmap =
           ExtBitmap.ConvolutionFilter(sourceBitmap, 
                         Matrix.Kirsch3x3Horizontal, 
                           Matrix.Kirsch3x3Vertical, 
                                  1.0, 0, grayscale);

 
    return resultBitmap;
}
public static double[,] Kirsch3x3Horizontal 
{ 
   get   
   {
       return new double[,]  
       { {  5,  5,  5, },  
         { -3,  0, -3, },  
         { -3, -3, -3, }, }; 
   } 
} 
public static double[,] Kirsch3x3Vertical
{ 
   get   
   { 
       return new double[,]  
       { {  5, -3, -3, },  
         {  5,  0, -3, },  
         {  5, -3, -3, }, }; 
   } 
}

Kirsch

Kirsch 

Kirsch Grayscale

Kirsch Grayscale

Related Articles and Feedback

Feedback and questions are always encouraged. If you know of an alternative implementation or have ideas on a more efficient implementation please share in the comments section.

I’ve published a number of articles related to imaging and images of which you can find URL links here:

32 Responses to “C# How to: Image Edge Detection”

Feed for this Entry Trackback Address
  1. 1 aliakbarp January 30, 2016 at 4:59 PM

    It’s really helpful.Thanks

    Reply

  1. 1 C# How to: Difference Of Gaussians | Software by Default Trackback on May 18, 2013 at 12:50 AM
  2. 2 C# How to: Image Median Filter | Software by Default Trackback on May 18, 2013 at 4:16 AM
  3. 3 C# How to: Image Unsharp Mask | Software by Default Trackback on May 18, 2013 at 12:18 PM
  4. 4 C# How to: Image Colour Average | Software by Default Trackback on May 18, 2013 at 9:48 PM
  5. 5 C# How to: Image Erosion and Dilation | Software by Default Trackback on May 19, 2013 at 10:24 AM
  6. 6 C# How to: Morphological Edge Detection | Software by Default Trackback on May 25, 2013 at 8:23 AM
  7. 7 C# How to: Boolean Edge Detection | Software by Default Trackback on June 1, 2013 at 2:09 AM
  8. 8 C# How to: Gradient Based Edge Detection | Software by Default Trackback on June 1, 2013 at 4:46 PM
  9. 9 C# How to: Image Cartoon Effect | Software by Default Trackback on June 2, 2013 at 4:13 PM
  10. 10 C# How to: Sharpen Edge Detection | Software by Default Trackback on June 7, 2013 at 5:11 AM
  11. 11 C# How to: Calculating Gaussian Kernels | Software by Default Trackback on June 8, 2013 at 10:59 AM
  12. 12 C# How to: Image Blur | Software by Default Trackback on June 9, 2013 at 10:19 PM
  13. 13 C# How to: Image Transform Rotate | Software by Default Trackback on June 16, 2013 at 10:40 AM
  14. 14 C# How to: Image Transform Shear | Software by Default Trackback on June 16, 2013 at 5:45 PM
  15. 15 C# How to: Compass Edge Detection | Software by Default Trackback on June 22, 2013 at 9:34 PM
  16. 16 C# How to: Oil Painting and Cartoon Filter | Software by Default Trackback on June 30, 2013 at 10:47 AM
  17. 17 C# How to: Stained Glass Image Filter | Software by Default Trackback on June 30, 2013 at 10:50 AM
  18. 18 C# How to: Image Convolution | Software by Default Trackback on June 30, 2013 at 3:54 PM
  19. 19 C# How to: Generate a Web Service from WSDL | Software by Default Trackback on June 30, 2013 at 4:08 PM
  20. 20 C# How to: Decoding/Converting Base64 strings to Bitmap images | Software by Default Trackback on June 30, 2013 at 4:13 PM
  21. 21 C# How to: Bitmap Colour Substitution implementing thresholds | Software by Default Trackback on July 6, 2013 at 4:33 PM
  22. 22 C# How to: Swapping Bitmap ARGB Colour Channels | Software by Default Trackback on July 6, 2013 at 5:02 PM
  23. 23 C# How to: Image filtering by directly manipulating Pixel ARGB values | Software by Default Trackback on July 8, 2013 at 2:57 AM
  24. 24 C# How to: Image ASCII Art | Software by Default Trackback on July 14, 2013 at 7:22 AM
  25. 25 C# How to: Weighted Difference of Gaussians | Software by Default Trackback on July 14, 2013 at 8:11 PM
  26. 26 C# How to: Image Boundary Extraction | Software by Default Trackback on July 21, 2013 at 10:23 AM
  27. 27 C# How to: Image Abstract Colours Filter | Software by Default Trackback on July 28, 2013 at 7:41 PM
  28. 28 C# How to: Fuzzy Blur Filter | Software by Default Trackback on August 9, 2013 at 6:39 AM
  29. 29 C# How to: Image Distortion Blur | Software by Default Trackback on August 9, 2013 at 10:13 PM
  30. 30 C# How to: Standard Deviation Edge Detection | Software by Default Trackback on August 8, 2015 at 8:10 AM
  31. 31 C# How to: Min/Max Edge Detection | Software by Default Trackback on August 9, 2015 at 11:30 AM

Leave a comment

« C# How to: Image Convolution
C# How to: Difference Of Gaussians »

Dewald Esterhuizen

View Dewald Esterhuizen's profile on LinkedIn

Blog Stats

  • 869,017 hits

Enter your email address to follow and receive notifications of new posts by email.

Join 228 other subscribers

Archives

RSS SoftwareByDefault on MSDN

  • An error has occurred; the feed is probably down. Try again later.
blog directory
Subscribe